年度別過去問題・類題
2022年度 2021年度 2019年度2018年度 2017年度 2016年度
2020年度
問題を選んで、〔GO!〕ボタンをクリックして下さい
● 似た問題のダウンロード


類題はダウンロードして、
印刷することができます。
ダウンロード
●〔2〕割合(還元と値引き)


同じX円の商品を買うのに、 ① 消費税を加えた値段から5%もどしてもらうのと、 ② 5%値引いてもらった値段に消費税を加えてはらうのでは、どちらが得か比べる問題。
そのあと、その理由を説明する。
ヒント
商品の値段がいくらでも答えは同じになるはずなので、商品の値段を計算がしやすい数字に決めて考えると、分かりやすくなります
解き方へGO!
商品の値段がいくらでも答えは同じになるはずなので、商品の値段を計算がしやすい数字に決めて考えると、分かりやすくなります
ビン入りのジュースを1ケース買いに、商店街へ行きました。商店街では、A店とB店で欲しいジュースを売っていました。どちらの店も定価は1ケースX円です。
A店では、カードでしはらうと10%が還元されます。つまり、消費税を加えた値段の10%がもどって来ます。
B店では、現金でしはらうと10%値引きしてくれます。つまり、定価の10%引きの値段に消費税がかかります。
食料品を買うときにかかる消費税は8%です。また、ジュース1ケースの定価は、1の位から100の位までの数字が全部0です。
(1)次の、①、②、③のうち正しいのはどれですか。
① A店で買う方が安い ② B店で買う方が安い ③ どちらも同じ
(2)A店、B店のそれぞれで買った場合に実際にしはらう金額をXの式で表して、(1)の理由を説明なさい。
(1)③
(2)どちらの店もX×0.972になって同じだから 計算へGO!
あるお店では、最初の週、商品の仕入れ値に3割の利益を見込んだ定価を付けて売り出しました。一つも売れないので、2割引きにして売ったところ全部売り切れました。
次の週、同じ商品に仕入れ値の2割の利益を見込んだ定価を付けて売り出しました。やっぱり一つも売れないので、1割引きにして売ったところ全部売れました。
商品の仕入れ値をX円として、最初の週と次の週に、商品が一つ売れたときの利益をXを使った式で表し、どちらの週の方がもうかったか答えなさい。
最初の週:X×0.04
次の週:X×0.08
次の週の方がもうかった 計算へGO!
●〔3〕(8)比例式
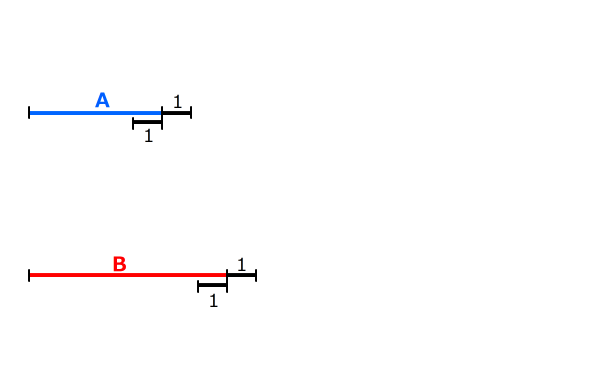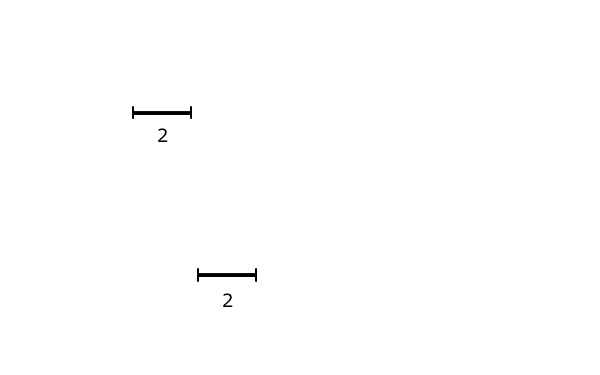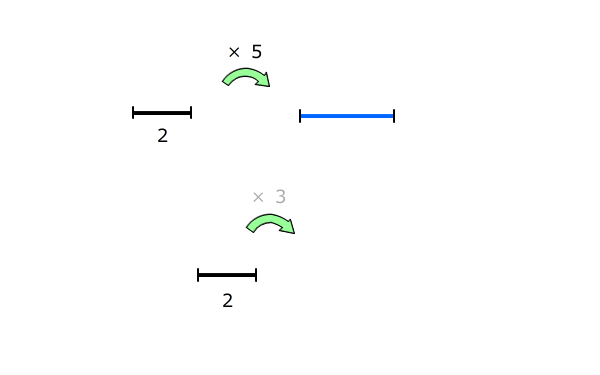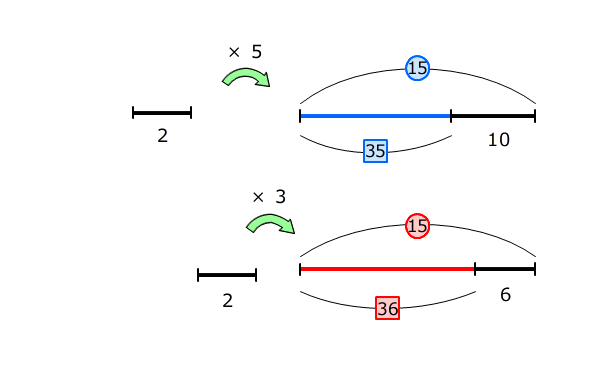
比例式に当てはまる数を求める問題
ヒント
問題文を読みかえると、倍数変化算の問題であることが分かります
解き方へGO!
問題文を読みかえると、倍数変化算の問題であることが分かります
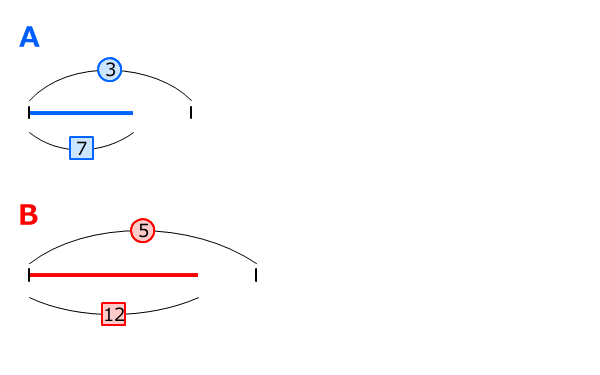
AとBは整数で、
(A+1):(B+1)=4:7
(A-1):(B-1)=5:9
です。このようなAとBのうち、Bが60以下のときのAを求めなさい。
31 (B:55) 解き方へGO!
AとBは整数で、
(A+1):(B+2)=5:8
(A-2):(B-1)=3:5
です。このようなAとBのうち、Bが60以下のときのAを求めなさい。
29 (B:46)
●〔4〕約数(おばあさんの年令)


64才のおあばあさんの年の数64は、令和2年の数2で割り切れる。
この次におばあさんの年の数が、令和の年の数で割り切れるのは何年後か求める問題。
その前に、62の約数を聞かれるので、それを利用する。
ヒント
おばあさんの年の数の中に令和の年の数は1つ分入っているので、残りの数がどうなれば、おばさんの年の数が令和の年の数で割り切れるか考える
解き方へGO!
おばあさんの年の数の中に令和の年の数は1つ分入っているので、残りの数がどうなれば、おばさんの年の数が令和の年の数で割り切れるか考える
(1)38の約数を小さい順にすべて答えなさい。
(2)令和2年5月1日現在、ジロー君のお父さんは40才です。お父さんの年の数40は、令和の年の数2で割り切れます。1年後には、お父さんの年の数は41になり、令和の年の数は3になって割り切れません。
次に、お父さんの年の数が令和の年の数で割り切れるのは、何年後ですか。
(1)1、2、19、38
(2)17年後 解き方へGO!
●〔5〕分数(単位分数)
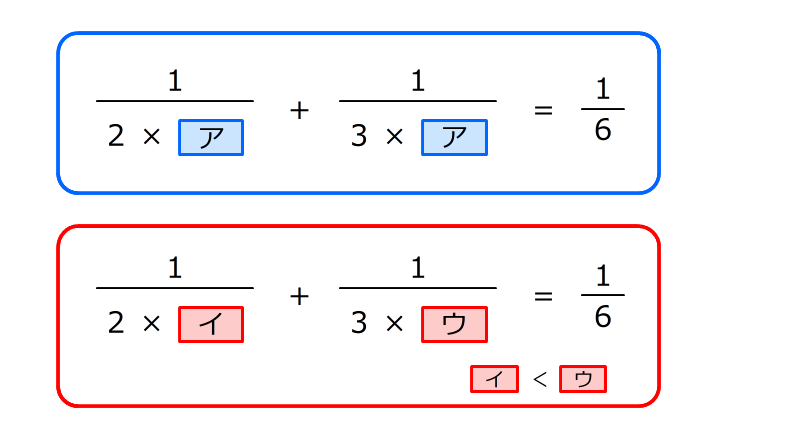
青の式のア、赤の式のイとウに入る数を求める問題
 解き方へGO!
解き方へGO!

(1)
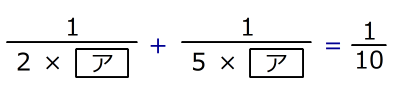 となる整数
となる整数 を求めなさい。
を求めなさい。(2)
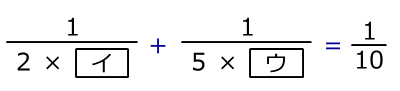 となる整数
となる整数 と
と を求めなさい。
を求めなさい。ただし、
 のほうが
のほうが よりも小さな数です。
よりも小さな数です。(1)
 :7
:7 (2)
 :6、
:6、 :12
:12
(2006年度〔6〕)
次の
 の中に、2から10までの整数を1回ずつ入れて、式を完成させてください。同じ記号には同じ整数がはいります。
の中に、2から10までの整数を1回ずつ入れて、式を完成させてください。同じ記号には同じ整数がはいります。(A)
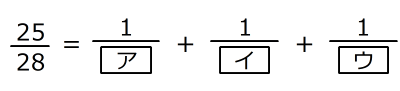
(B)
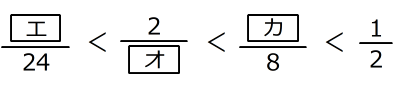
(
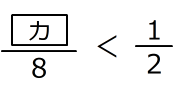 は
は  より
より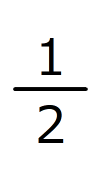 が大きいことを表します。)
が大きいことを表します。)(C)

ア:2 イ:4 ウ:7 エ:5 オ:9
カ:3 キ:6 ク:8 ケ:10
(ア、イ、ウと、キ、クは順序がちがってもよい) 解き方へGO!
●〔6〕(13)時計算

 、
、 の角度が同じときの時刻を求める問題
の角度が同じときの時刻を求める問題
解き方へGO!
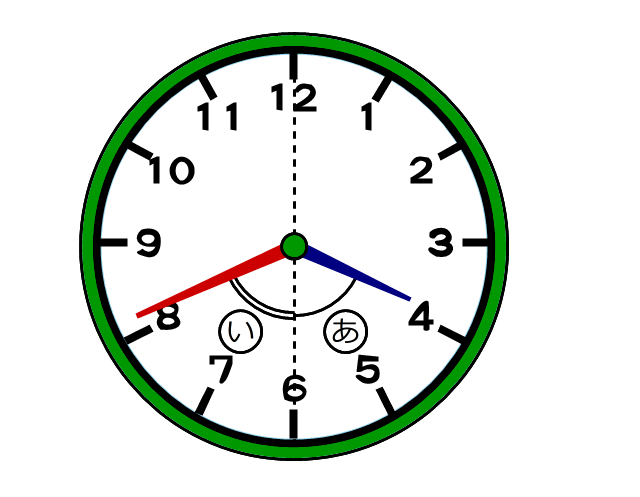
午後3時すぎに時計を見たら、右の図の
 と
と の2つの角度が同じでした。
の2つの角度が同じでした。このときの時刻は午後3時何分ですか。
午後3時
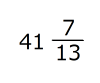 分
解き方へGO!
分
解き方へGO!●〔7〕(14)体積
●〔8〕面積(三角形と半円)
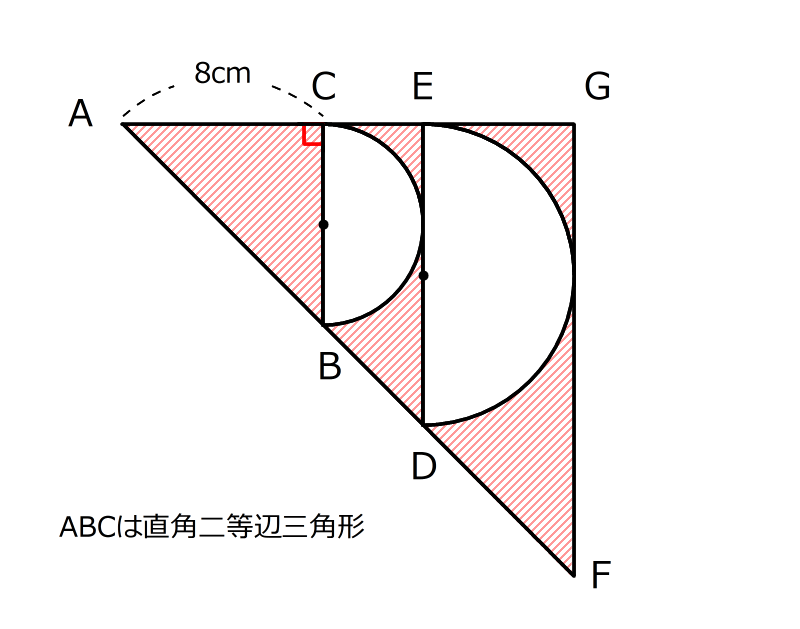
赤いところと白いところの面積の差を求め、円周率を3にしたらそれがどうなるか答える問題
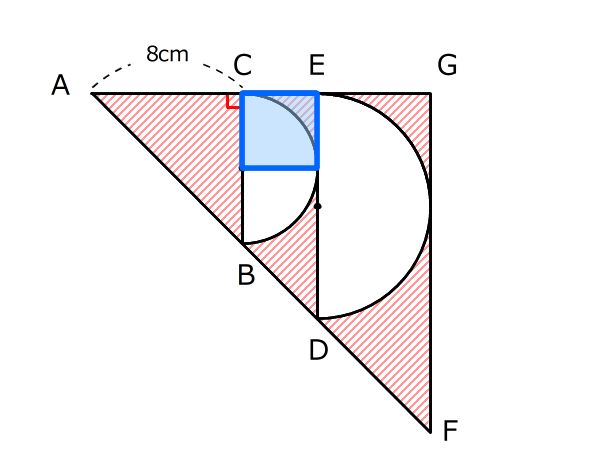 ヒント
ヒント
青い四角は正方形になります。
解き方へGO!
 ヒント
ヒント青い四角は正方形になります。
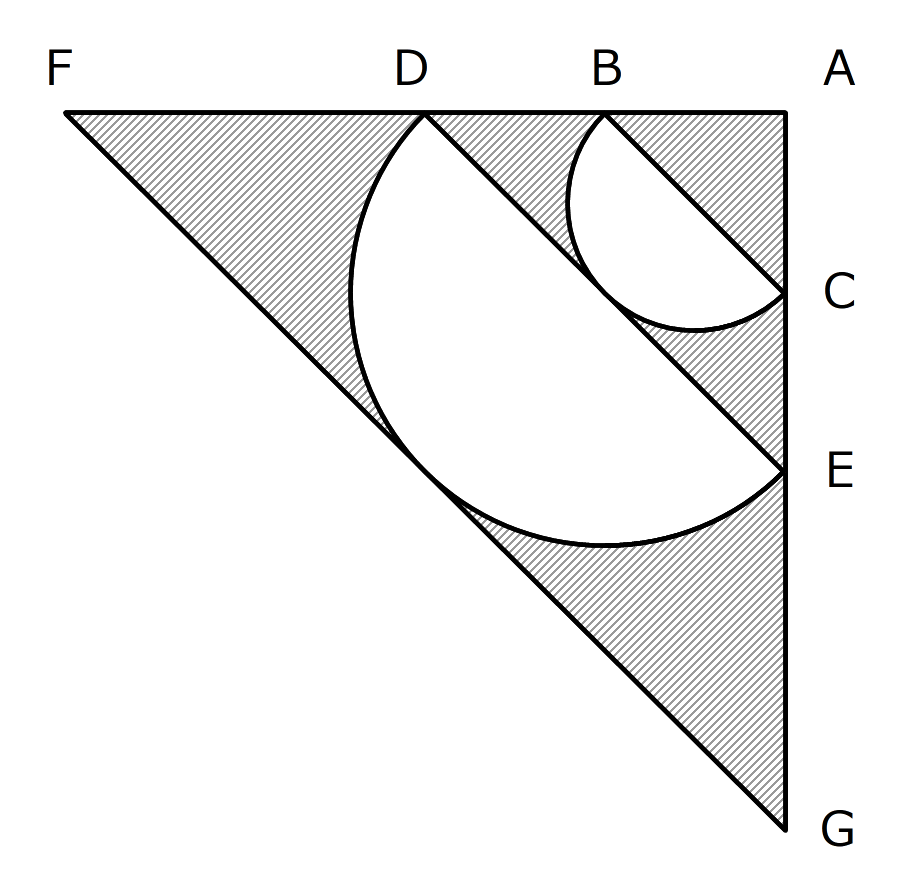
図の三角形ABC、ADE、AFGは、どれも角Aが90度の直角二等辺三角形です。辺BC、DEが直径の半円が、三角形ADE、AFGの中にちょうど入っています。
図の色の付いた部分の面積をP㎠、半円2つの面積の合計をQ㎠とするとき、次の問いに答えなさい。BCの長さは4cmです。
(1)円周率を3.14として計算するとき、PとQの差を求めなさい。
(2)円周率を3として計算すると、P、Qの差はどうなりますか。次の中から選びなさい。
ア.Pの方が大きいまま
イ.Pの方が大きかったのが、同じになった
ウ.Pの方が大きかったのに、Qの方が大きくなった
エ.Qの方が大きいまま
オ.Qの方が大きかったのが、同じになった
カ.Qの方が大きかったのに、Pの方が大きくなった
(1) 1.2㎠ (2) ア 解き方へGO!
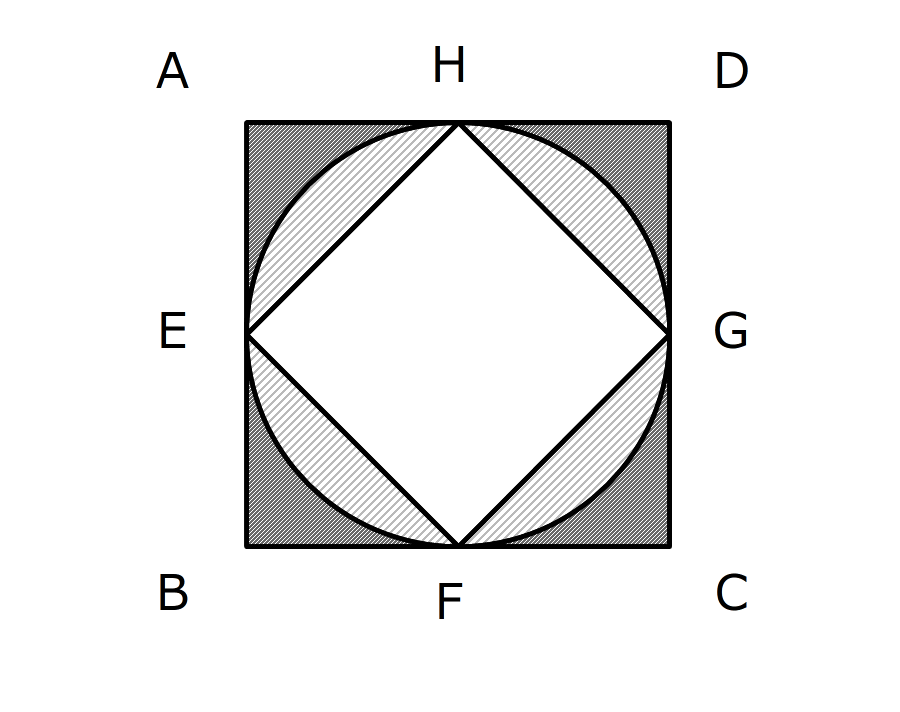
一辺の長さが8cmの正方形ABCDの中に円がぴったりと入っています。また、その円の中に正方形EFGHがぴったりと入っています。
大きな正方形と円で囲まれた色のこい部分をP、円と小さい正方形で囲まれた色のうすい部分をQとします。
(1)PとQの面積の差を求めなさい。円周率は3.14とします。
(2)円周率を3にしたとき、PとQの面積の差はどうなりますか。次の中から選びなさい。
ア.Pの方が大きいまま
イ.Pの方が大きかったのが、同じになった
ウ.Pの方が大きかったのに、Qの方が大きくなった
エ.Qの方が大きいまま
オ.Qの方が大きかったのが、同じになった
カ.Qの方が大きかったのに、Pの方が大きくなった
(1) 4.48㎠
(2) オ 計算へGO!
●〔9〕(17)角度
角度を求める問題
ヒント
2つの三角形が相似であることを利用します。だから、「どういう三角形が相似になるか」知っている必要があります。
解き方へGO!
2つの三角形が相似であることを利用します。だから、「どういう三角形が相似になるか」知っている必要があります。
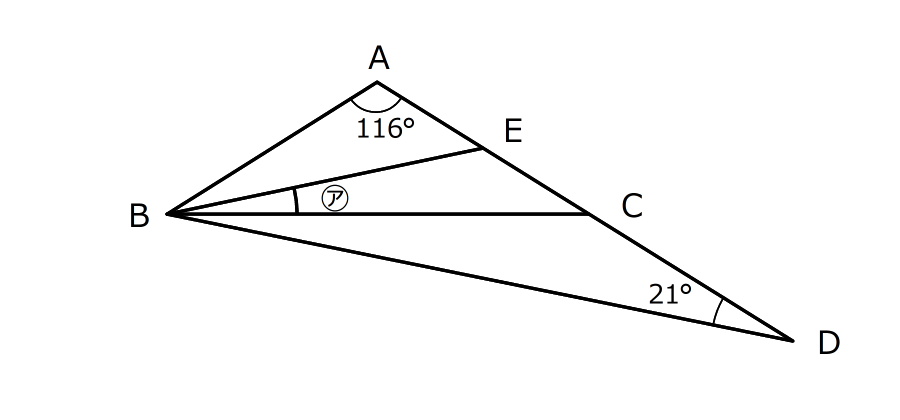
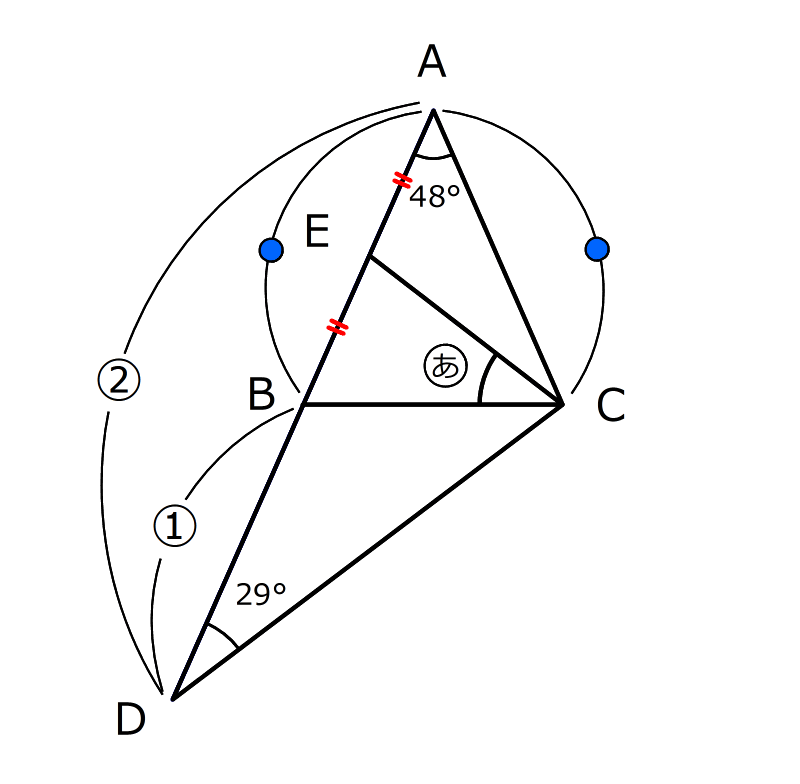
図のようなAB=ACである二等辺三角形ABCがあります。
辺ACの真ん中の点をEとし、辺ACをCの方にのばした直線の上に点Dを、AD:DC=2:1となるようにとりました。このとき、角㋐の大きさを求めなさい。
11度 計算へGO!
●〔10〕地震のグラフ
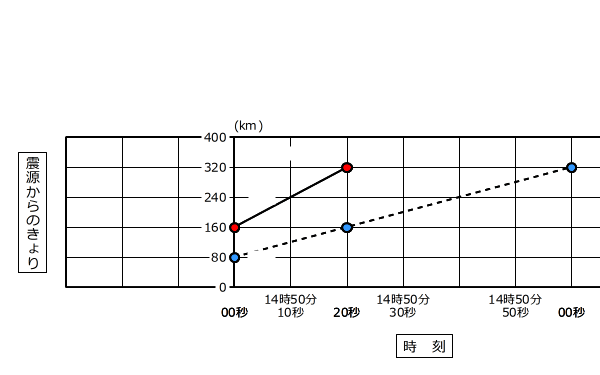

地震波のグラフを使って、地震が起きた時刻を求める問題
ヒント
地震が起きた時刻は、震源からのきょりが0kmの地点がゆれ始める時刻
解き方へGO!
地震が起きた時刻は、震源からのきょりが0kmの地点がゆれ始める時刻
●〔11〕(20)面積(おうぎ形)
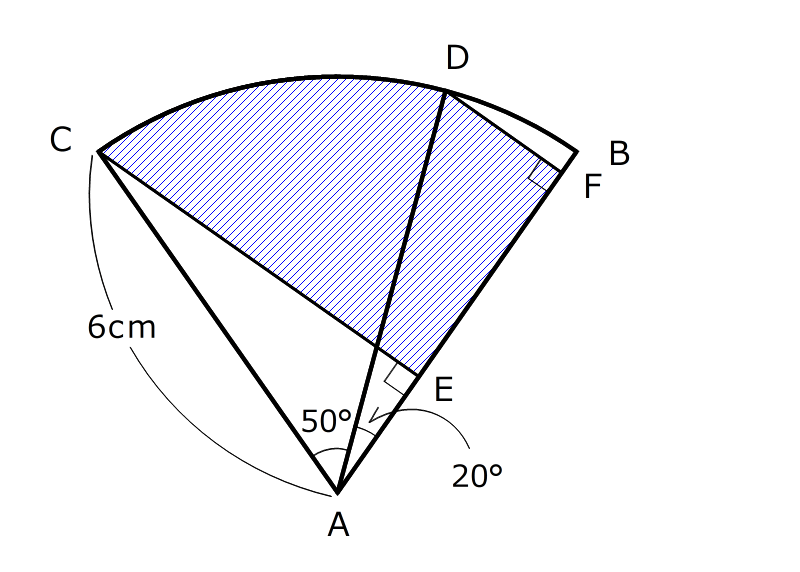
面積を求める問題
ヒント
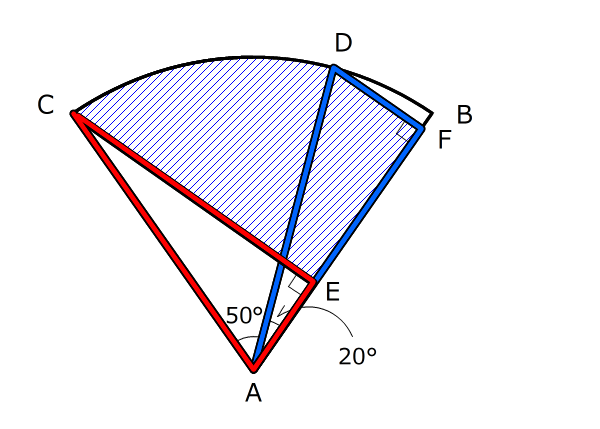 2つの三角形が合同であることを利用します。だから、「どういう三角形が合同になるか」知っている必要があります。
解き方へGO!
2つの三角形が合同であることを利用します。だから、「どういう三角形が合同になるか」知っている必要があります。
解き方へGO!
 2つの三角形が合同であることを利用します。だから、「どういう三角形が合同になるか」知っている必要があります。
2つの三角形が合同であることを利用します。だから、「どういう三角形が合同になるか」知っている必要があります。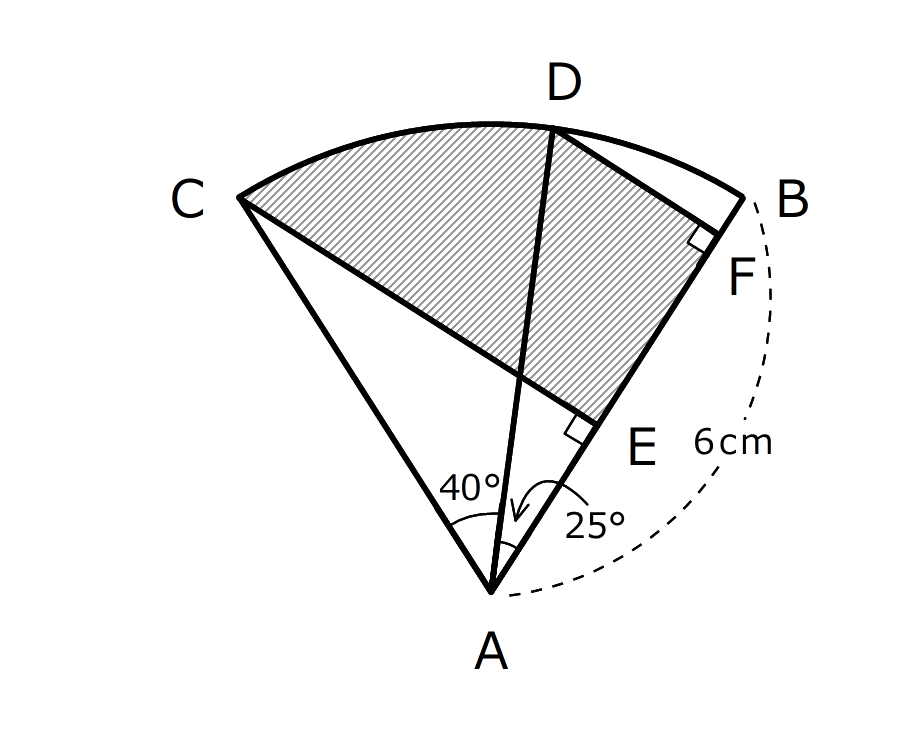
点Aを中心とする半径6cm、中心角65°のおうぎ形ABCがあります。おうぎ形の弧BCの上に点Dがあります。CとDからそれぞれ直線ABに垂直な線を引きました。しゃ線をつけた部分の面積を求めなさい。
12.56c㎡ 解き方へGO!
●〔12〕(21)作図

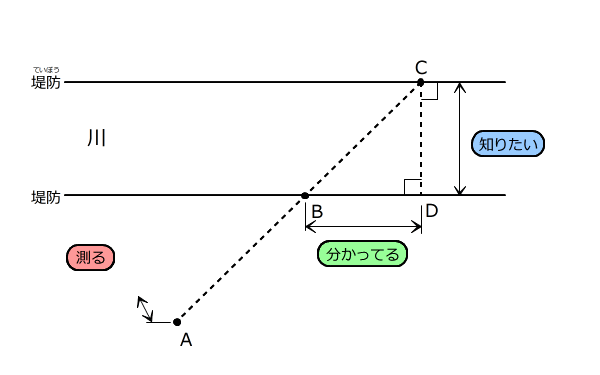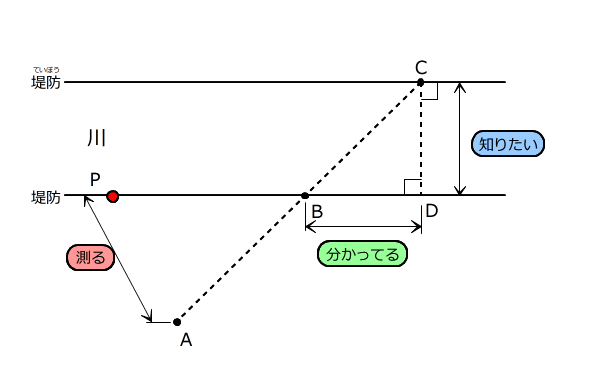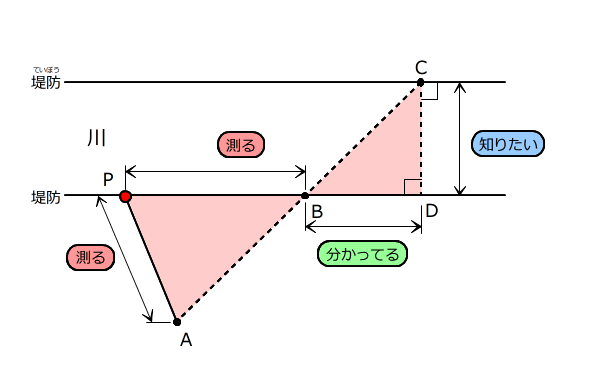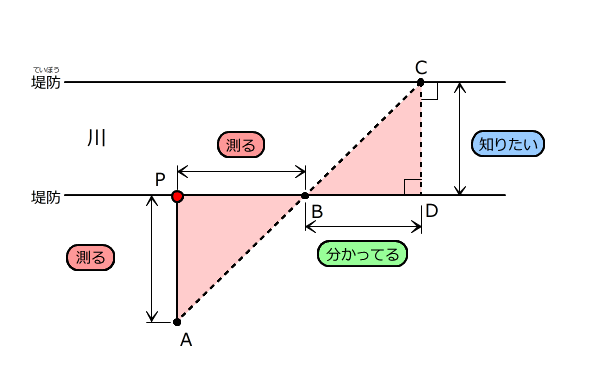
Aからの長さを測ったら川のはばが分かるような場所を作図する問題
 ヒント
ヒント
ちょうちょの形の相似な三角形ができるような場所を探します。
解き方へGO!
 ヒント
ヒントちょうちょの形の相似な三角形ができるような場所を探します。
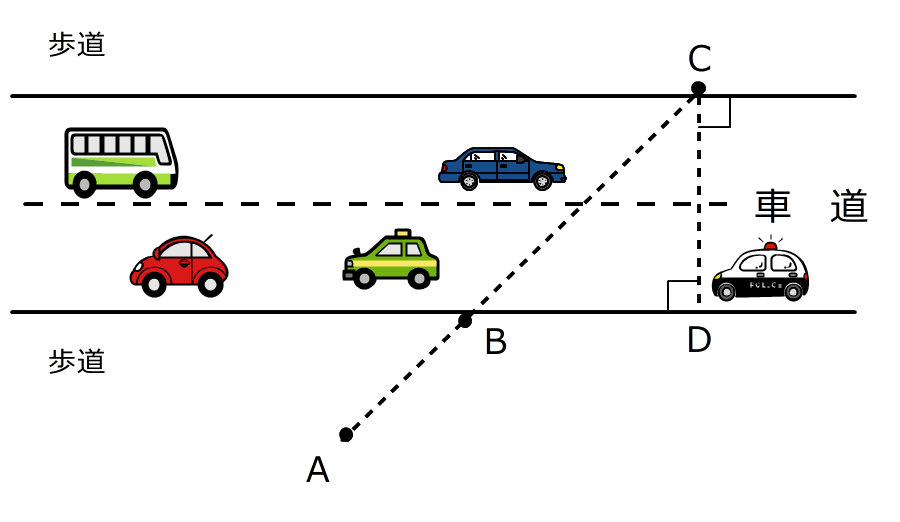
町の真ん中を大通りがまっすぐに通っています。車道のはばを測りたいのですが、ひっきりなしに車が走っているので危なくて測れません。
そこで、B君とC君が車道をはさんで歩道の車道に近いはしに立ち、A君はB君と同じ側の歩道の車道から一番はなれた所に立ちました。3人は一直線に並んでいます。また、D君はB君と同じ側の歩道の車道に近いはしで、C君のちょうど反対側に立ちました。B君とD君のきょりは分かっています。
B君の横の方の車道に近いはしに地点Pを見つけ、そこからA君、B君までのきょりが分かれば、安全に車道のはばを測ることができます。
この地点Pを、作図して見つけなさい。
(注意)
・1番目にかいた円の中心(コンパスの針をさしたところ)に×印とその横に①を書く。その中心を使ってかいた円または円の一部にも①と書く。
・2番目にかいた円の中心に×印とその横に②を書く。その中心を使ってかいた円または円の一部に②と書く。
・以下、円または円の一部をかくたびに同じように書く。
・作図するのに使った線は消さずに残しておくこと。
・定規は直線を引くために用い、目盛りを使用しないこと。
解き方へGO!

リンゴの実がなりました。食べたいのですが、高いところになっていてとることができません。今にも落ちて来そうなので、ショウ君は落ちてくるまで待つことにしました。待つのに一番いい場所を点Pとし、作図で求めなさい。
(注意)
・1番目にかいた円の中心(コンパスの針をさしたところ)に×印とその横に①を書く。その中心を使ってかいた円または円の一部にも①と書く。
・2番目にかいた円の中心に×印とその横に②を書く。その中心を使ってかいた円または円の一部に②と書く。
・以下、円または円の一部をかくたびに同じように書く。
・作図するのに使った線は消さずに残しておくこと。
・定規は直線を引くために用い、目盛りを使用しないこと。
作図へGO!

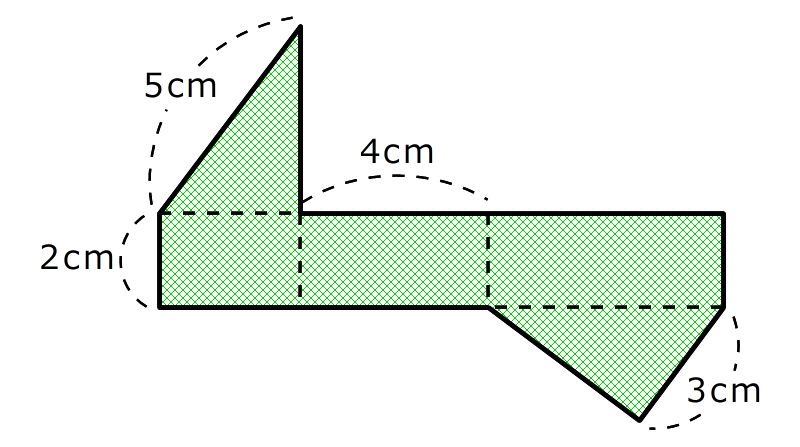
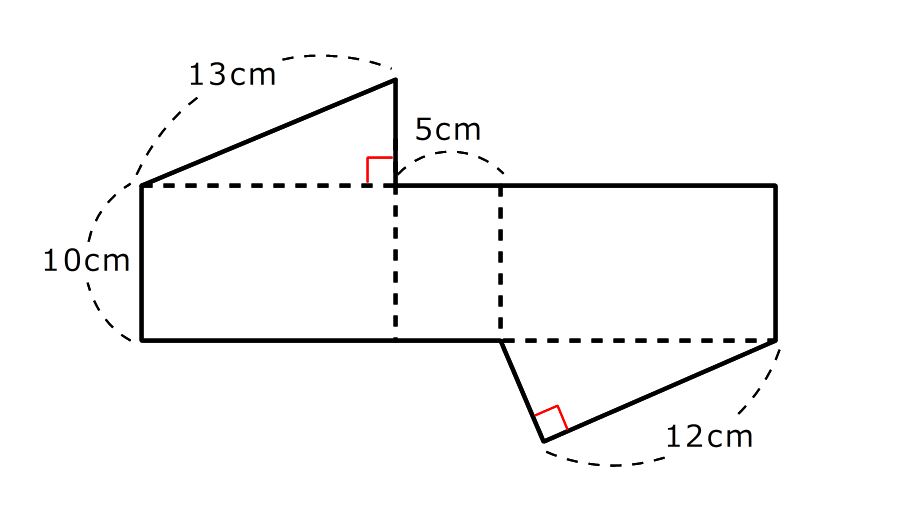 右の図は、ある立体の展開図です。3つの長方形と2つの合同な直角三角形でできています。この立体の体積を求めなさい。
右の図は、ある立体の展開図です。3つの長方形と2つの合同な直角三角形でできています。この立体の体積を求めなさい。

