年度別過去問題・類題
２０２１年度 ２０２０年度 ２０１９年度 ２０１８年度２０１９年度
〔１〕（２）円の面積 〔１〕（３）逆数・逆算 〔１〕（４）対称図形の角度〔１〕（５）割合の応用 〔２〕円の回転移動 〔３〕立方体の展開図
〔４〕時計算 〔５〕あまりのある割り算 〔６〕集合算
● 似た問題のダウンロード
●〔１〕（２）円の面積
〔１〕（２）円の面積
過去問題の解き方
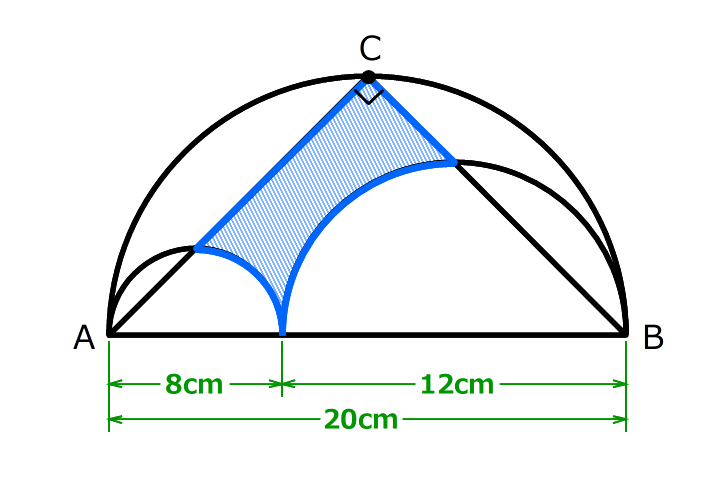直径２０ｃｍの半円があります。ＡとＢは、直径の両端です。Ｃは円周上にあって、ＡとＢから同じ距離のところにあります。Ｃの角度は直角です。この半円の中に、直径が重なるように、直径８ｃｍと直径１２ｃｍの半円を書きました。
影をつけた部分の面積を求めなさい。
３３.１８㎠ （類題１）の解き方
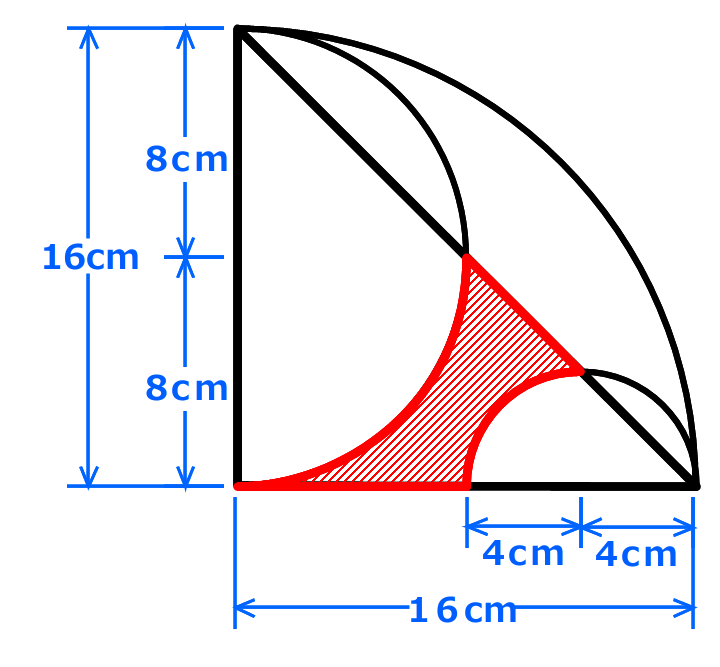図のように、半径が１６ｃｍで中心角が９０度のおうぎ形の中に、半径が８ｃｍと半径が４ｃｍの半円を書きました。影を付けた部分の面積を求めなさい。
２５.２㎠ （類題２）の計算
●〔１〕（３）逆数・逆算
〔１〕（３）逆数・逆算
過去問題の解き方
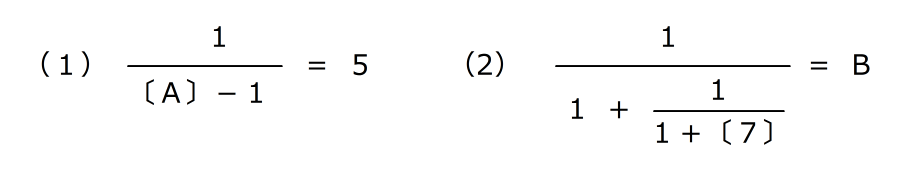
〔Ｘ〕は、Ｘの逆数を表します。たとえば、〔４〕＝
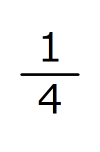、〔０.５〕＝２です。（１） のＡ、（２）のＢに当てはまる数を答えなさい。
（１）
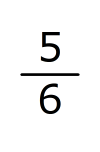（２）
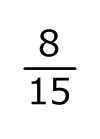（類題１）の解き方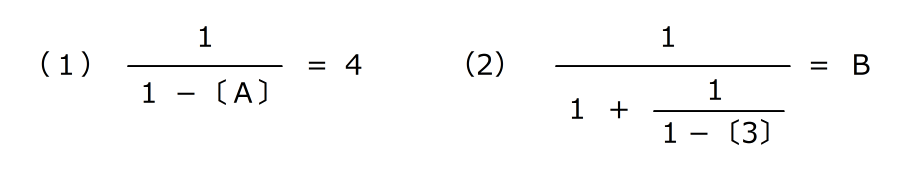
〔Ｘ〕は、Ｘの逆数を表します。たとえば、〔６〕＝
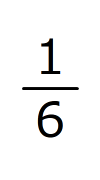、〔０.１２５〕＝８です。（１） のＡ、（２）のＢに当てはまる数を答えなさい。
（１）
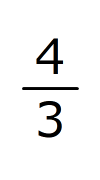（２）
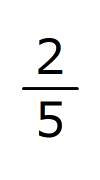
●〔１〕（４）対称図形の角度
〔１〕（４）対称図形の角度
過去問題の解き方
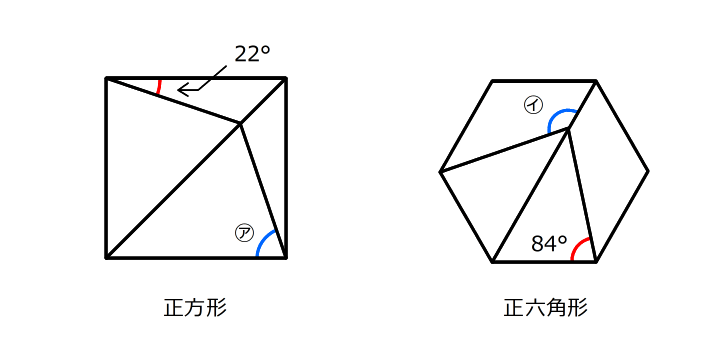
右の図の、㋐、㋑の角度を求めなさい。
㋐：６８° ㋑：１４４° （類題１）の計算
●〔１〕（５）割合の応用
〔１〕（５）割合の応用
過去問題の解き方
３匹の犬、ダダ、ゴン、ポチの体重を量りました。ゴンはダダよりも３.６ｋｇ重く、ポチとダダを合わせた体重とゴンの体重の違いは、ポチの体重の
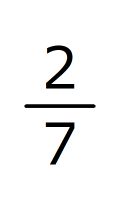でした。ポチの体重を求めなさい。ただし、ポチの体重は２通り考えられます。５.０４ｋｇ、２.８ｋｇ （類題１）の解き方
シュン、ダイキ、ソウタの３人が、持っているモンスターカードの枚数を比べました。シュンはダイキより２８枚多く持っていました。また、ソウタとダイキのカードを合わせた枚数と、シュンの枚数との差はソウタの持っている枚数の
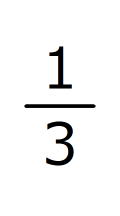倍でした。ソウタが持っている枚数は２通りが考えられます。その２通りの枚数を答えなさい。４２枚、２１枚 （類題２）の計算
●〔２〕円の回転移動
〔２〕円の回転移動
過去問題の解き方
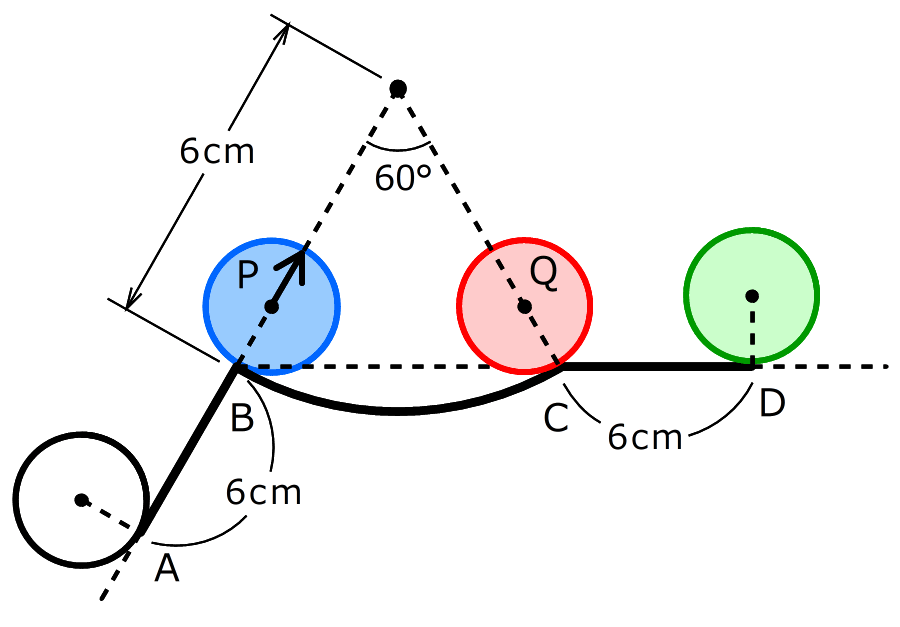右の図のように、半径１ｃｍの円をＡからＤまで太線に沿って転がします。（１）円の中心が動く道のりを求めなさい。答えは、小数第２位を四捨五入して答えなさい。
（２）円の中心がＰに来たとき、円に書いた矢印は、弧の中心を向いていました。円の中心がＱに来たときの矢印の向きを図に書きなさい。また、矢印と点線の角度を求めなさい。
（１）１８.８ｃｍ
（２）真上向き、３０度 （類題１）の計算
●〔３〕立方体の展開図
〔３〕立方体の展開図
過去問題の解き方
●〔４〕時計算
〔４〕時計算
過去問題の解き方
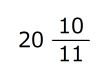分後、長針は短針の９０度後ろのところに来ます。（１）今、長針と短針が作る角度のうち、小さい方の角度を答えなさい。
（２）今が午前中だとすると、今は何時か答えなさい。
（１）１５５度 （２）午前４時５０分 （類題１）の解き方
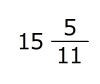分前、時計の長針と短針の作る角度は１８０度でした。（１）今、長針と短針が作る角度は何度ですか。
（２）今は、午後何時何分ですか。
（１）９５度（２）午後５時１０分 （類題２）の計算
●〔５〕あまりのある割り算
〔５〕あまりのある割り算
過去問題の解き方
あるスーパーがミカンを袋に入れて売ります。
７個入りは５００円で、１０個入りは７００円で売ります。ミカン全部を７個入りにすると、ミカンは１個余ります。全部を１０個入りにすると、４個余ります。全部を７個入りにして売って売り切れた場合と、全部を１０個入りにして売って売り切れた場合とでは、売り上げの差は１３００円になります。次の問いに答えなさい。
（１）ミカンは全部でいくつありますか。
（２）売り上げを最も多くしようとすると、売り上げはいくらになりますか。
（１）７６４個 （２）５４５００円 （類題１）の計算
●〔６〕集合算
〔６〕集合算
過去問題の解き方
ある小学校で、６年生の家が飼っているペットについて調べました。どこの家もペットを飼っています。ペットは、犬、猫、ハムスター、金魚です。次のことが分かりました。
（ア）犬、猫、ハムスター、金魚のうち、３種類以上を飼っている家はありません。
（イ）２種類を飼っている家は２０軒です。
（ウ）猫と金魚の両方を飼っている家はありません。
（エ）犬とハムスターの両方を飼っている家は、犬を飼っている家の
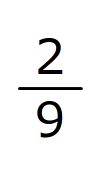、ハムスターを飼っている家の
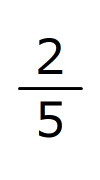です。（オ）犬を飼っていない家は、３９軒です。
（カ）犬、猫、金魚のうち２種類を飼っている家の数は、ハムスターだけを飼っている家より５軒だけ少ない数です。
次の問いに答えなさい。
（１）犬とハムスターの両方を飼っている家は何軒ですか。
（２）猫か金魚を飼っている家は何軒ですか。
（３）６年生の生徒は何人ですか。
（１）１０軒 （２）３４軒 （３）８４人 （類題１）の解き方
数字をたくさん書きました。どれも、２、３、５、７の倍数です。ただし、２、３、５、７全部の数の公倍数と、２、３、５、７のうち３つの数の公倍数はありません。数は次の条件に当てはまります。
（ア）５と７の公倍数はない
（イ）２、３、５、７のうち２つの数の公倍数は３６個です。
（ウ）６の倍数は、２の倍数の
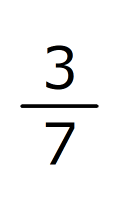、３の倍数の
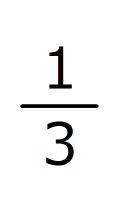だけあります。（エ）奇数は６０個あります。
（オ）２、５、７のうち２つの数の公倍数の個数は、３だけの倍数の個数より２７個少ない数です。
次の問いに答えなさい。
（１）６の倍数はいくつありますか。
（２）５か７の倍数はいくつありますか。
（３）数字は全部でいくつありますか。
（１）２１個 （２）３３個 １０９個 （類題２）の解き方
