年度別過去問題・類題
２０２１年度２０２０年度
〔Ⅰ〕（２）割合（消費税） 〔Ⅰ〕（３）植木算（ちょうちんの数） 〔Ⅱ〕（１）円の回転移動〔Ⅱ〕（２）円柱の体積・表面積 〔Ⅲ〕直方体の切断 〔Ⅳ〕分数、場合の数
● 似た問題のダウンロード
●〔Ⅰ〕（２）割合（消費税）
〔Ⅰ〕（２）割合（消費税）
過去問題の解き方
家族６人でショッピングモールへ行き、お好み焼きを１枚ずつ食べました。帰りに、家に帰ってからのおやつ用にもう１枚ずつ買いました。値段は、消費税をふくめて全部で８５０２円でした。
ショッピングモールで食べたお好み焼きには１０％の消費税が、家に持ち帰ったお好み焼きには８％の消費税がかかりました。また、消費税の金額は円単位の数字で、１円より小さな金額はありませんでした。
消費税がかかる前のお好み焼き１枚の値段を求めなさい。
６５０円 （類題１）の解き方
マイさんは、両親と妹、弟といっしょにスーパーへ行き、タイ焼きを一つずつ食べました。それから、家で留守番をしているおじいちゃんとおばあちゃんへのお土産にひとつずつ買って帰りました。値段は全部で１１４９円でした。
タイ焼きは、スーパーで食べると１０％の消費税がかかり、家へ持ち帰ると８％の消費税がかかります。また、消費税の金額はちょうど円単位の数字でした。
消費税がかかる前のタイ焼き１つの値段を求めなさい。
１５０円 （類題２）の計算
●〔Ⅰ〕（３）植木算（ちょうちんの数）
〔Ⅰ〕（３）植木算（ちょうちんの数）
過去問題の解き方
道に沿って木を植えます。まずサクラを５ｍごとに８本植えます。その間にツツジを１.２ｍごとに植えます。最初のツツジは、１本目のサクラから７０ｃｍのところに植えます。
１本目から８本目のサクラまでには、サクラとツツジが同じところに植えるようになることはありません。
（１）ツツジは全部で何本植えますか。
（２）最後のツツジは、８本目のサクラから何ｃｍのところに植えますか。
（３）ツツジがサクラに近すぎないように、サクラから５０ｃｍ以内のところには、ツツジを植えないことにしました。この場合、植えるツツジは何本になりますか。
（１）２９本 （２）７０ｃｍ （３）２３本 （類題１）の解き方
●〔Ⅱ〕（１）円の回転移動
〔Ⅱ〕（１）円の回転移動
過去問題の解き方
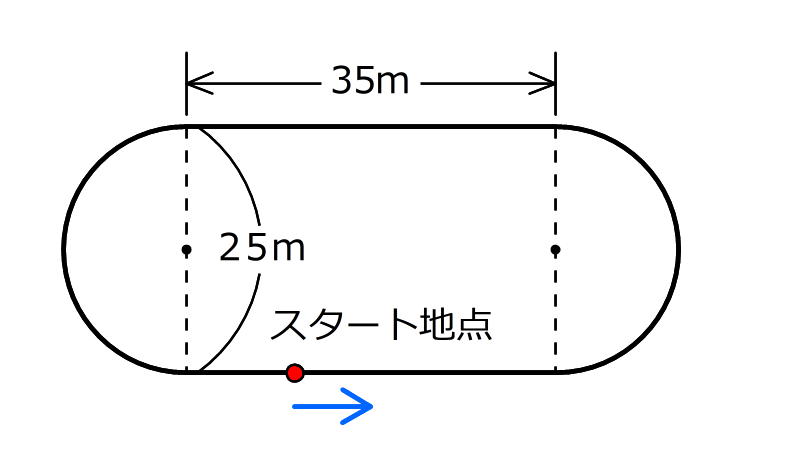
サキさんとアイさんが、図のようなコースを一輪車で競走しました。コースの丸い部分は直径２５ｍの半円で、直線部分の長さは３５ｍです。サキさんの一輪車の車輪の周りの長さは１８０ｃｍで、アイさんのは１５０ｃｍです。また、競走している間、車輪はすべることなく転がります。
（１）サキさんがコースを１周する間に、車輪は何回転しますか。
（２）２人はスタート地点を同時に出発しました。２人は、矢印の向きに、１秒間に車輪を１回転させながら進みました。途中、サキさんは３回転び、転んだ場所から再び走り始めるまで、１回につき１５秒かかりました。
サキさんとアイさんは同時にゴールしました。２人は、スタートしてからゴールするまでに、コースを何周しましたか。ただし、スタート地点とゴール地点が同じ場所であるとは限りません。
（１）８２.５回 （２）
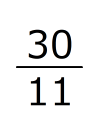周
（類題１）の計算
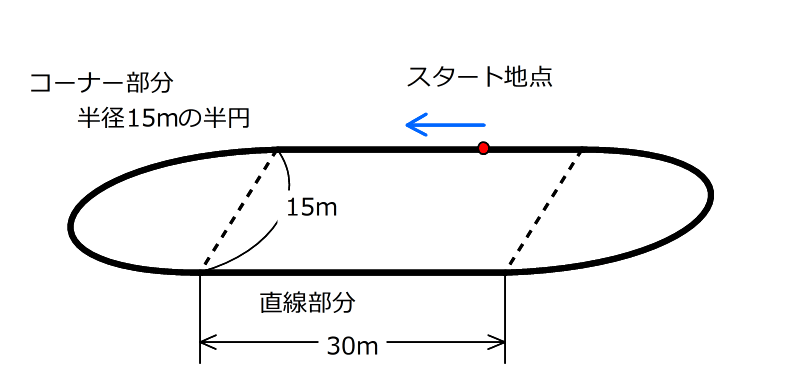
サトシとケンタが競歩で速さを競いました。競歩はかけっことはちがって、片方の足は地面に付いていないといけません。だから、進む道のりは歩数に歩はばを掛けた数になります。
サトシの歩はばは９０ｃｍ、ケンタの歩はばは８５ｃｍで、２人とも１秒間に２歩進みます。
（１）ケンタは何歩でコースを１周しますか。
（２）今回は、ミノルが審判をし、地面から両足がはなれたら、その場所から歩き直します。一度足がはなれると、戻って再び歩き始めるまでに２０秒かかります。２人は同時にスタートし、同時にゴールしました。でも、サトシは途中で２回、両足を地面からはなしてしまいました。２人は、スタートしてからゴールするまでに、コースを何周しましたか。ただし、スタート地点とゴール地点が同じ場所であるとは限りません。
（１）１２６歩 （２）
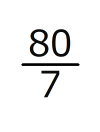周
●〔Ⅱ〕（２）円柱の体積・表面積
〔Ⅱ〕（２）円柱の体積・表面積
過去問題の解き方
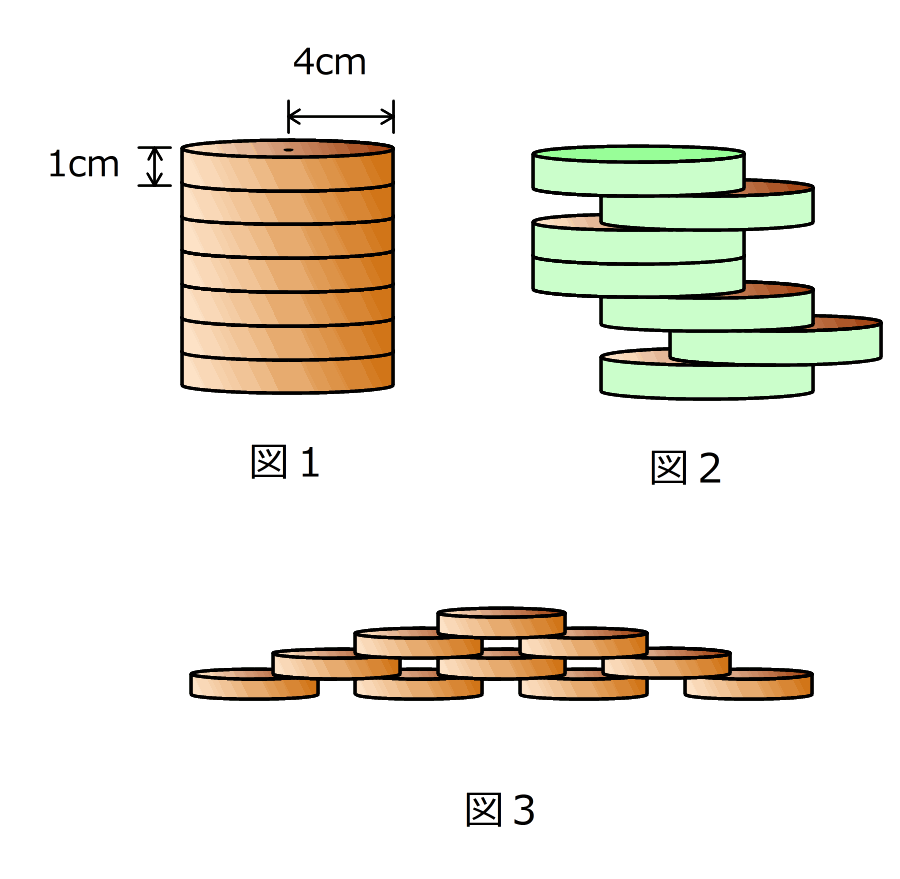
〔A〕底面が半径４ｃｍの円で、高さが１ｃｍの円柱の形の積み木があります。
（１）図１のように、この積み木７個を積み重ねて大きな円柱を作りました。この大きな円柱の体積と表面積を求めなさい。
（２）この大きな円柱の表面に色をぬり、その後図２のように積み木を横にずらしました。ずれている部分はどこも、底面の円の面積の４分の３だけ重なるようにずらしてあります。積み木の色のぬっていない部分の面積を求めなさい。
〔B〕同じ積み木を、今度は図３のように台の上に積みました。１番上の段には１個、上から２段目には２個、上から３段目には３個と、下の段にいくにつれて個数が１つずつ増えるように積んであります。また、重なっている部分はどれも、底面の円の面積の４分の１だけが重なるようにしてあります。
（３）積み木を１５０個使うとき、何段まで積むことができますか。
（４）今積んだ積み木の、上から見える部分と、台にふれている部分の面積の合計を求めなさい。
５.０４ｋｇ、２.８ｋｇ （類題１）の解き方
●〔Ⅲ〕直方体の切断
〔Ⅲ〕直方体の切断
過去問題の解き方
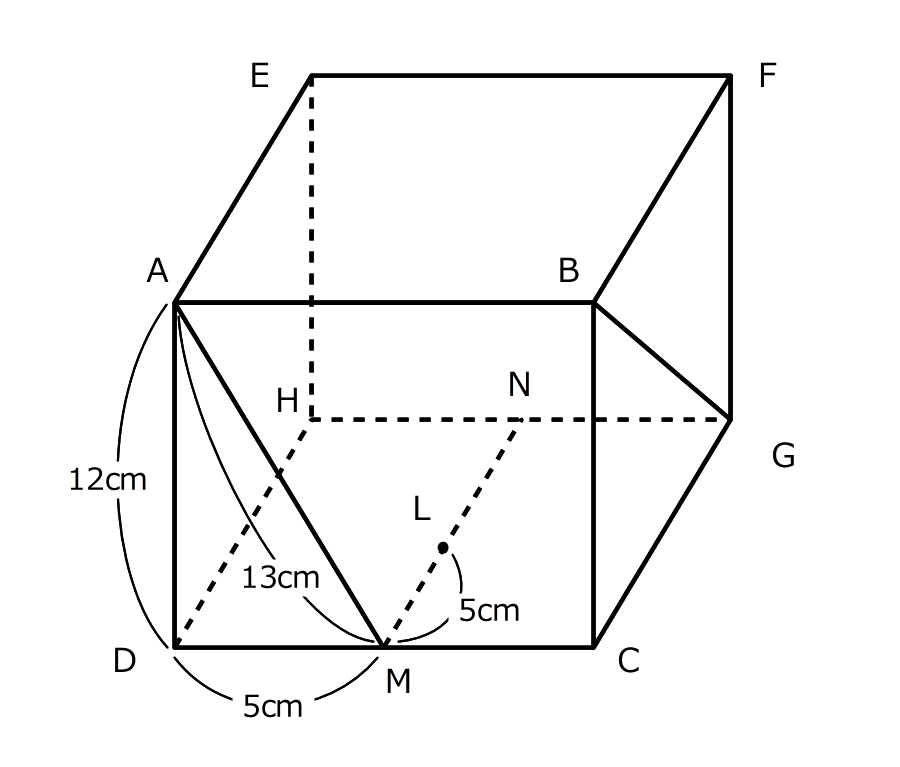右の図の直方体で、点ＭとＮは、それぞれ辺ＤＣとＨＧの真ん中の点です。また、ＭＮの上に点Ｌがあって、ＡＤ＝１２ｃｍ、ＤＭ＝５ｃｍ、ＡＭ＝１３ｃｍです。三角形ＡＤＭと三角形ＧＣＢは相似の関係にあって、三角形ＧＣＢの１番短い辺はＢＣです。（１）辺ＧＣとＢＧの長さを求めなさい。
（２）三角形ＡＮＢ、ＡＬＢ、ＡＬＮ、ＢＬＮで囲まれた立体ＡＬＢＮの体積を求めなさい。
（３）① 三角形ＡＮＢの面積を求めなさい。
② 立体ＡＬＢＮの表面積を求めなさい。
（１）ＧＣ：
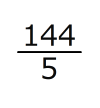ｃｍ ＧＢ：
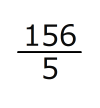ｃｍ（２）４７６㎤
（３）①：１５６㎠ ②：
㎠
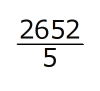（類題１）の解き方
