〔Ⅲ〕直方体の切断(類題1)

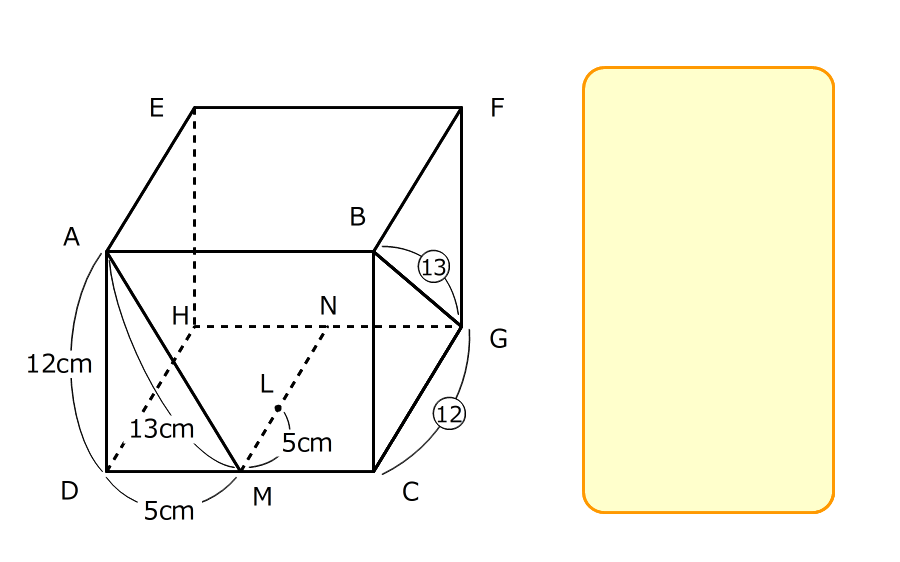
(1)辺GC、BGの長さを求める
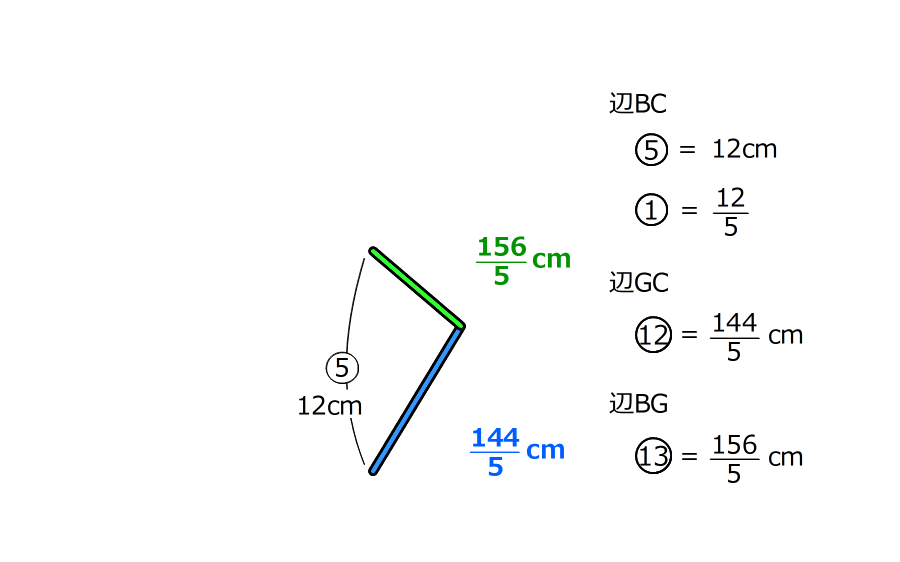
1.相似の関係にある三角形の辺の長さの比は同じなので、GC:CB:BG=12:5:13
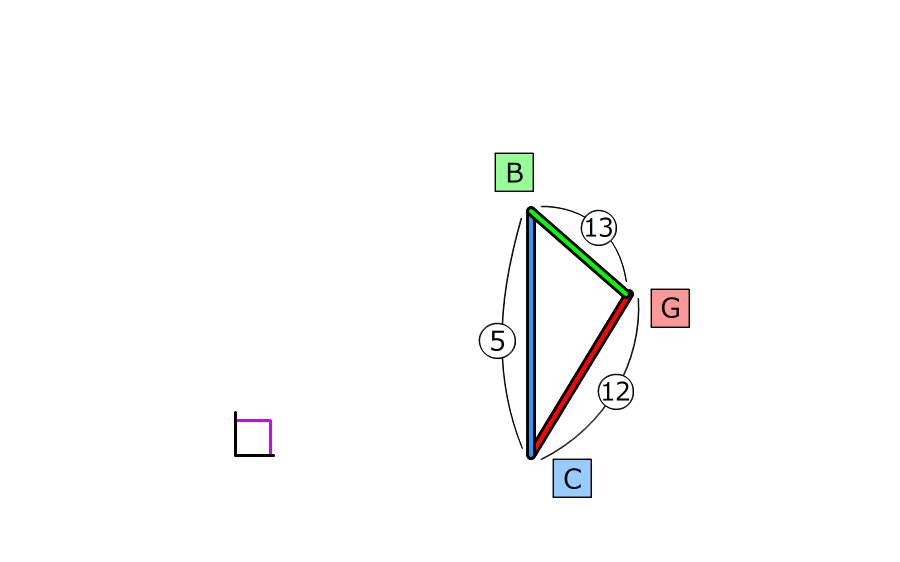

2.BCの長さがADと同じで12cmなので、⑤=12cmだと分かる

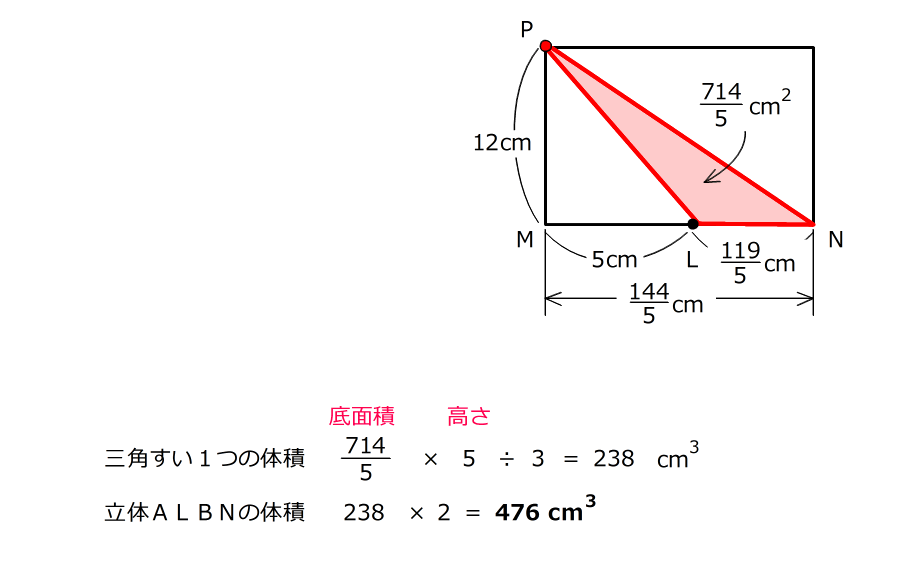
(2)立体ALBNの体積を求める
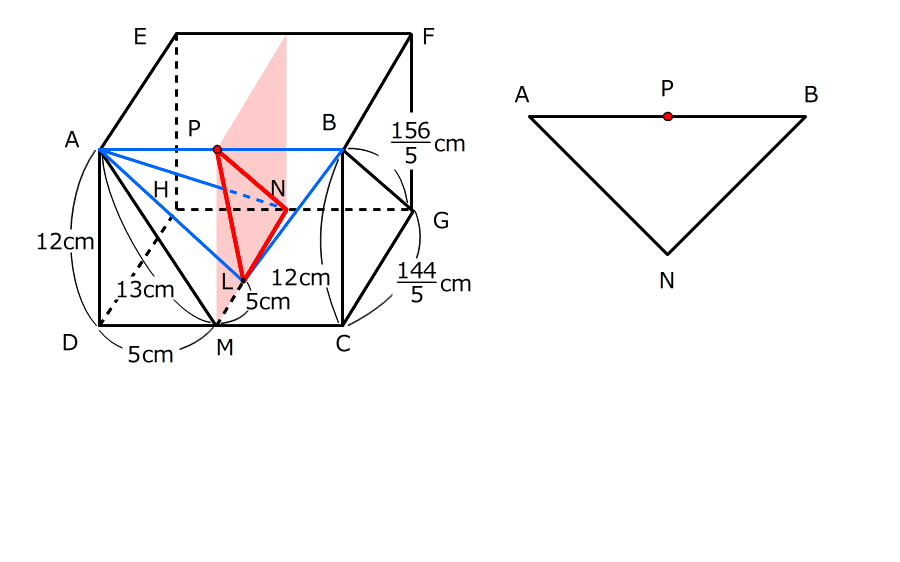
3.ABの真ん中に点Pを作る
立体ALBNを、点MとPを通って、四角形BCGFに平行な平面で切ると、三角形PLNが底面で同じ高さの三角すいが2つできる
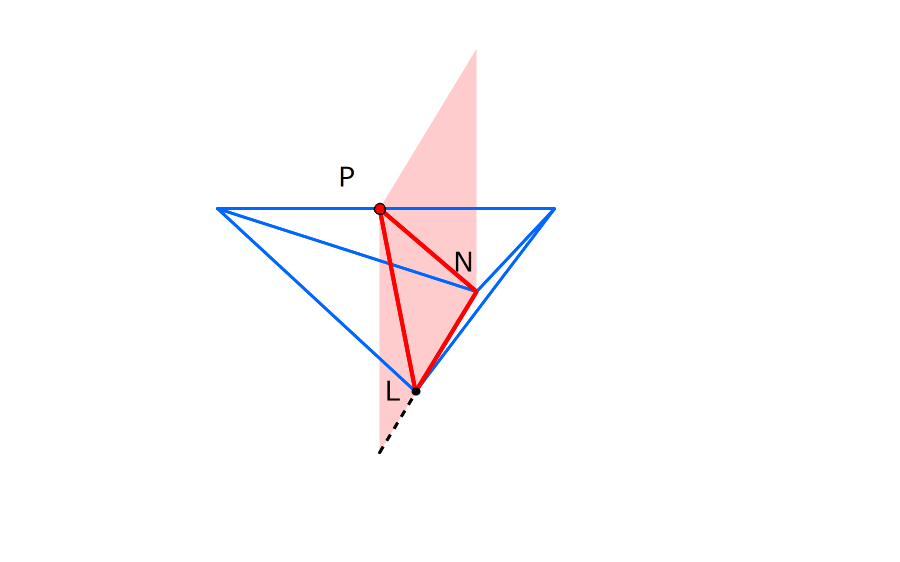

4.立体ALBNを2つに割ってできる三角すいは、
底辺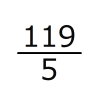 cmで高さ12cmの三角形が底面で、高さは5cm
cmで高さ12cmの三角形が底面で、高さは5cm
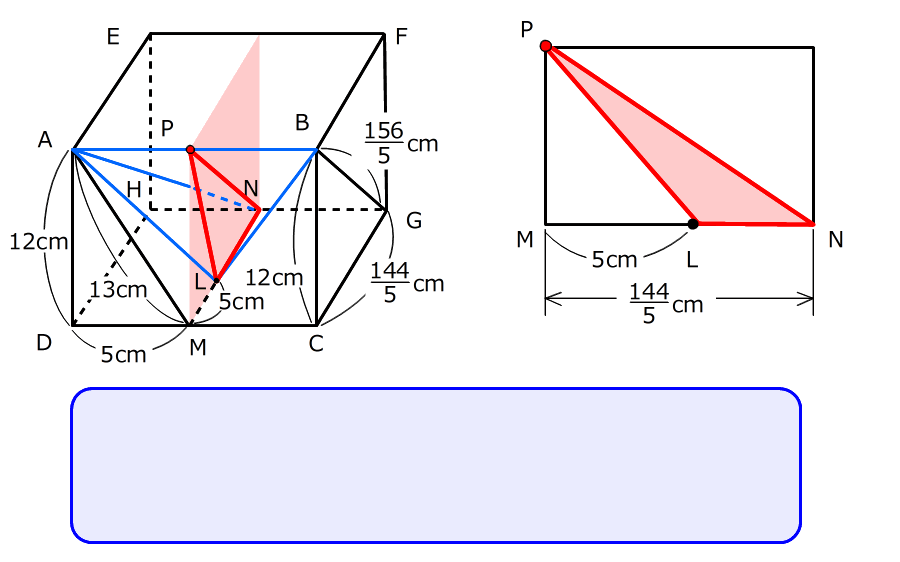


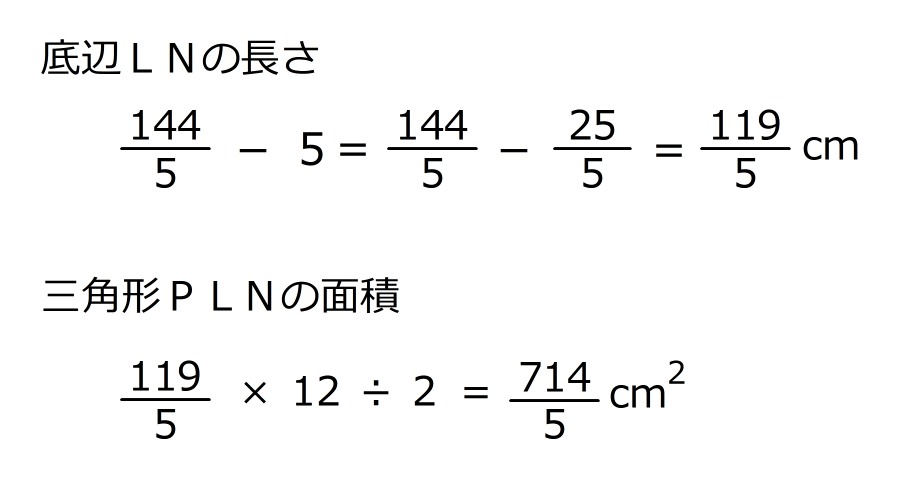
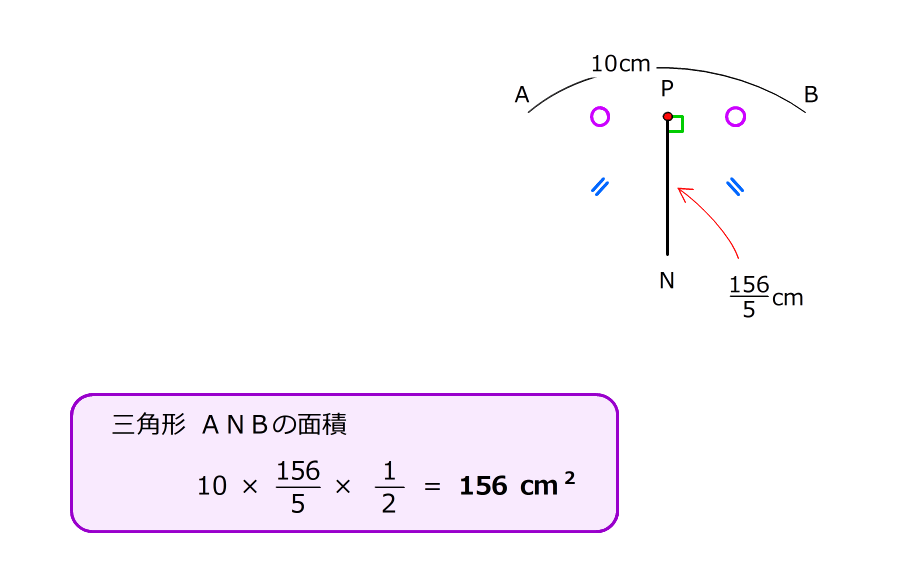
(3)① 三角形ANBの面積を求める
5.底辺ABは10cm、AN=BNの二等辺三角形で、PはABの真ん中の点なので、PNが高さになる

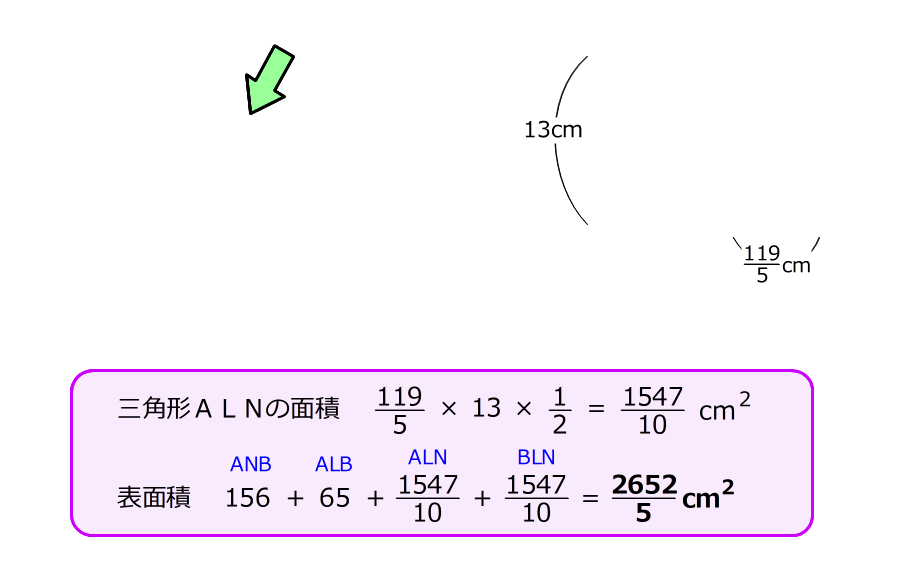
(3)② 立体ALBNの表面積を求める
6.表面は4つの三角形で、三角形ANBは①で求めたので残りを順に求める
三角形ALBの底辺はABで10cm、高さはPLで5cm
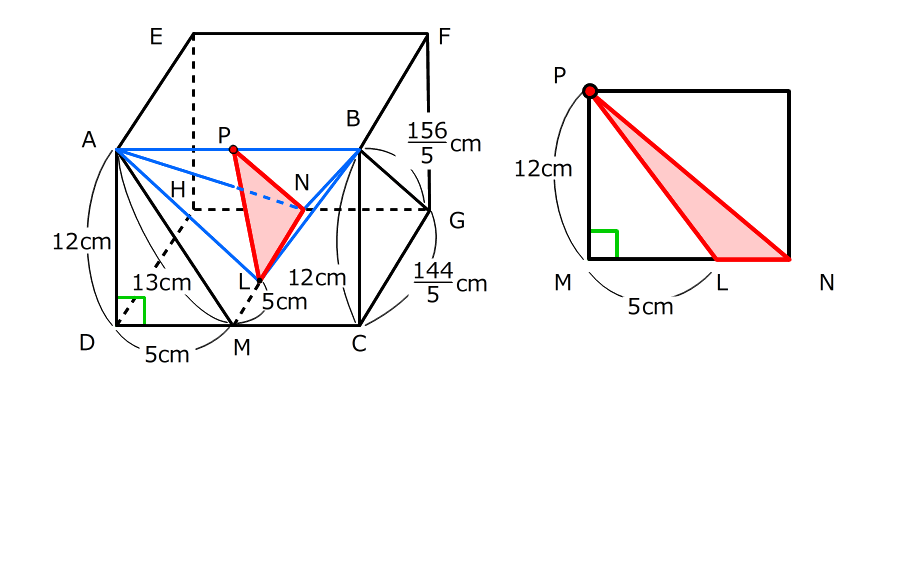
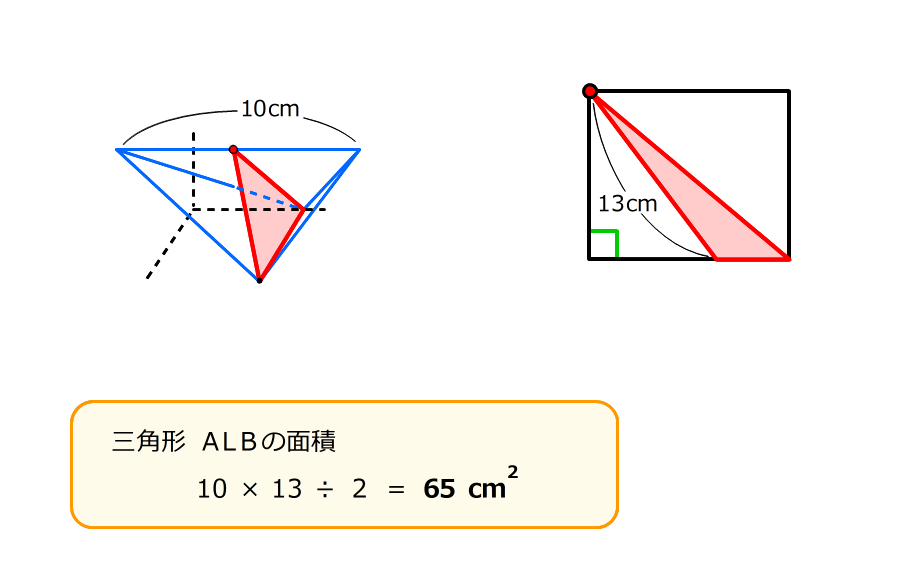

7.三角形ALNとBLNは同じ形
底辺はLNで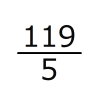 cm、高さはAMで13cm
cm、高さはAMで13cm
これまでに求めた4つの三角形の面積を加えると、立体ALBNの表面積になる
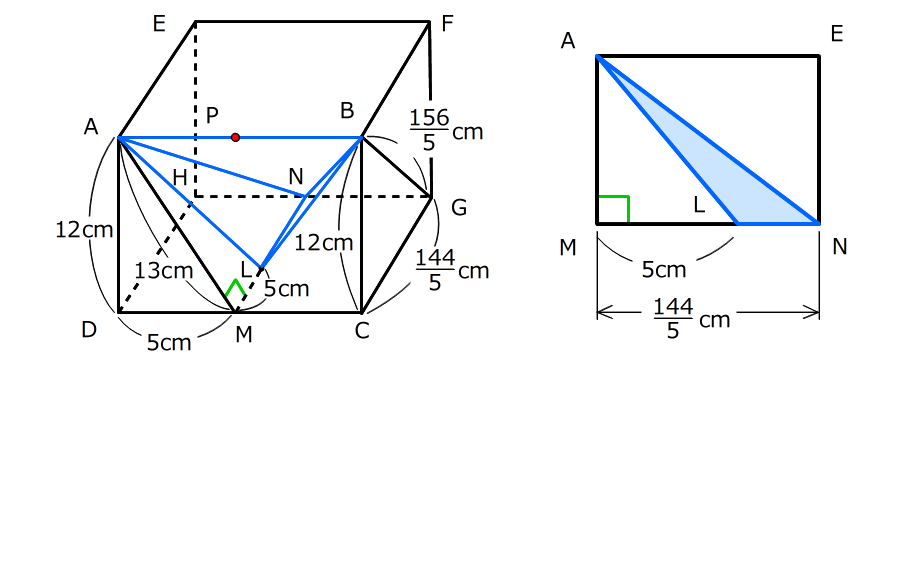



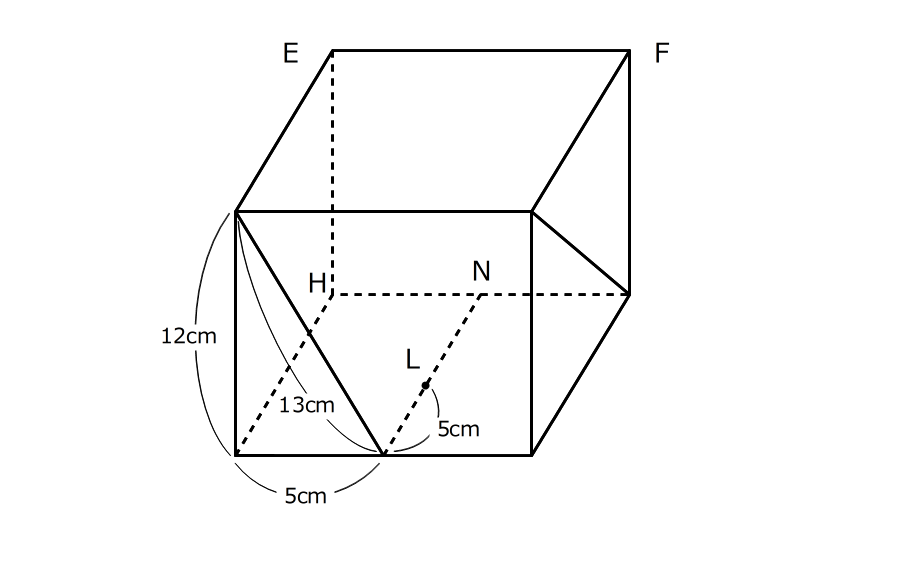
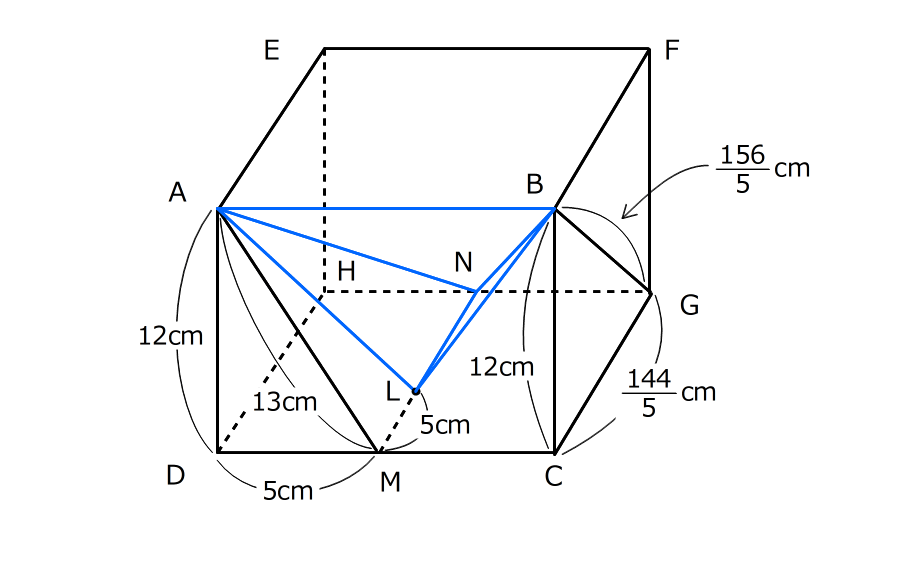
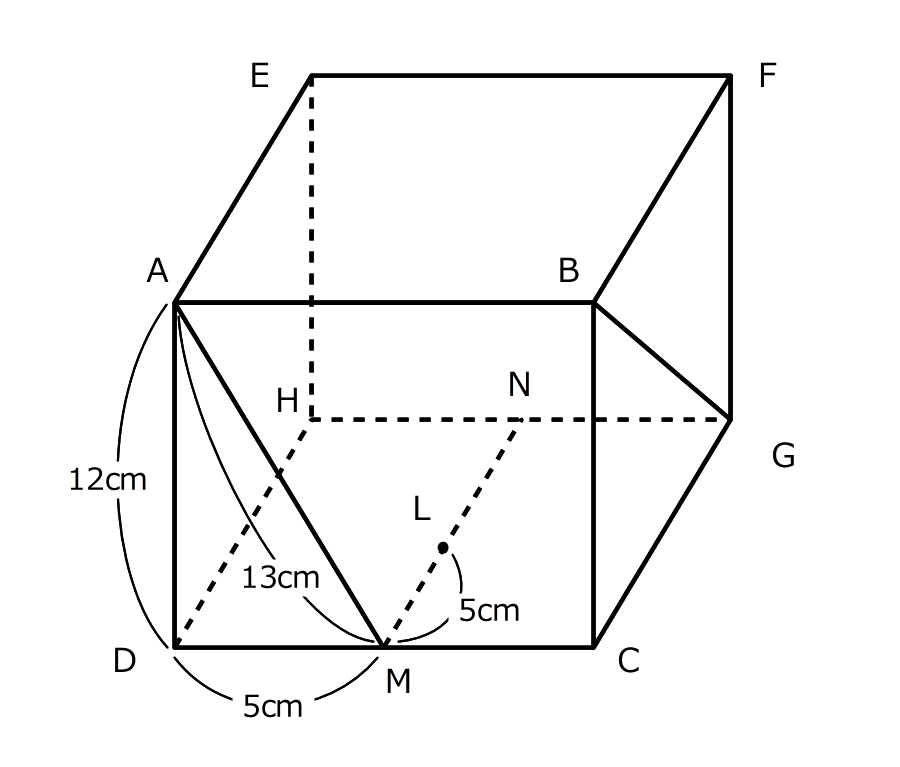 右の図の直方体で、点MとNは、それぞれ辺DCとHGの真ん中の点です。また、MNの上に点Lがあって、AD=12cm、DM=5cm、AM=13cmです。三角形ADMと三角形GCBは相似の関係にあって、三角形GCBの1番短い辺はBCです。
右の図の直方体で、点MとNは、それぞれ辺DCとHGの真ん中の点です。また、MNの上に点Lがあって、AD=12cm、DM=5cm、AM=13cmです。三角形ADMと三角形GCBは相似の関係にあって、三角形GCBの1番短い辺はBCです。

