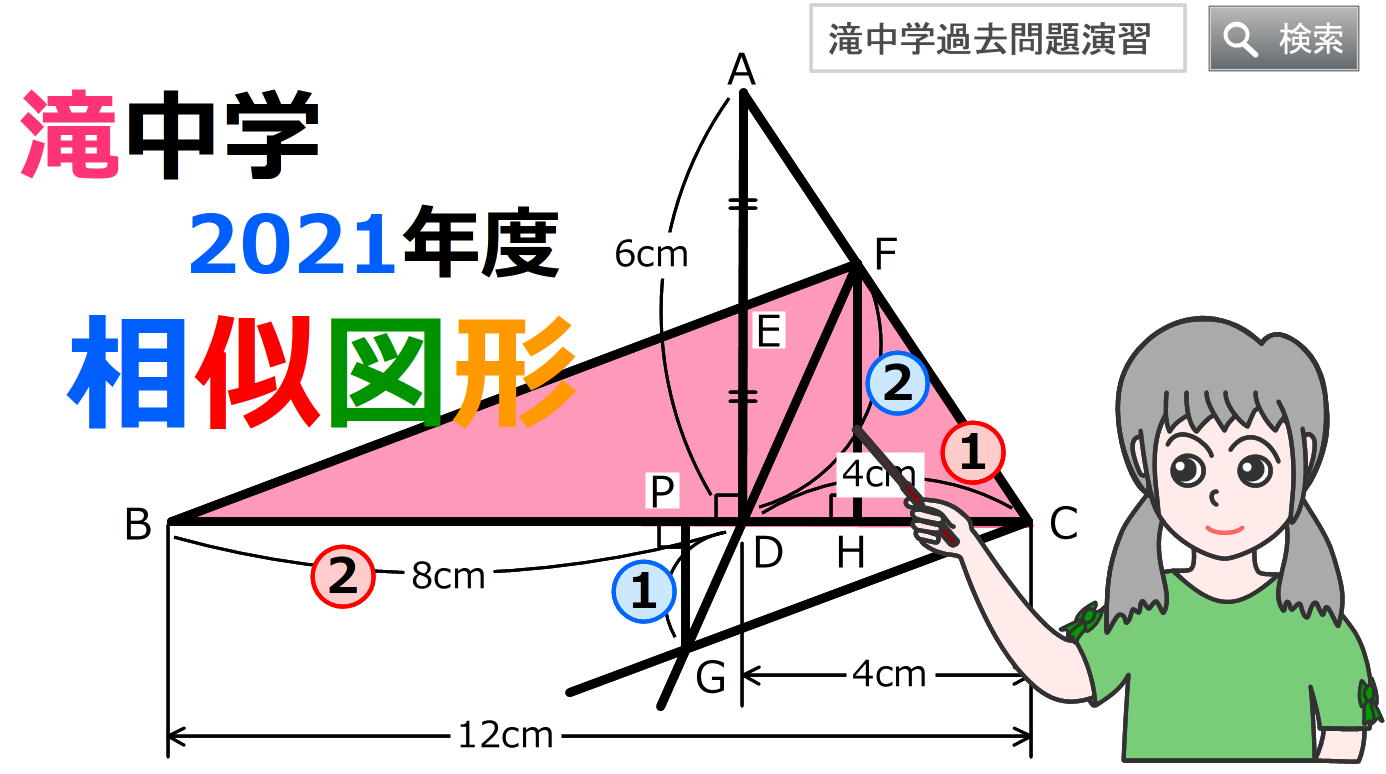
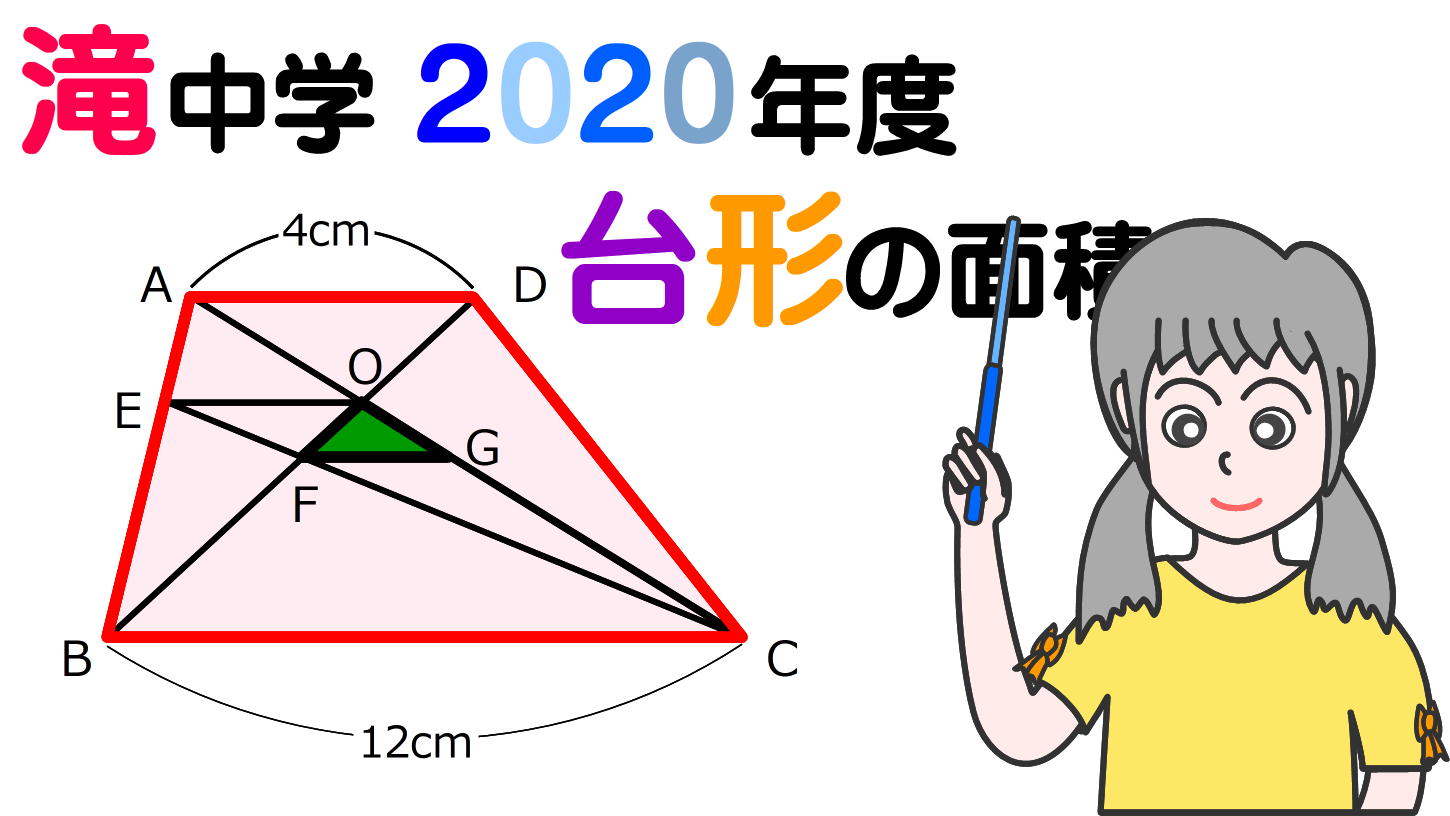
〔４〕相似図形の面積（過去問題）
（図）
問題の確認
図の四角形ＡＢＣＤは長方形で、角ＡＨＢは４５度、三角形ＣＧＨの面積は１８c㎡です。
このとき、（１）ＢＣの長さ、 （２）ＤＥ、ＥＦ、ＦＢの長さの比、 （３）四角形ＥＦＣＧの面積 を求めます。
１．（１）ＢＣの長さを求める
角Ｂが直角で、角ＡＨＢが４５度なので、角ＨＡＢも４５度で、三角形ＡＢＨは直角二等辺三角形です。だから、ＢＨの長さは１６cmになります。
また、ＤＣとＡＢが平行なので、三角形ＣＧＨと三角形ＢＡＨは山の形の相似になって、三角形ＣＧＨは二等辺三角形です。
２.三角形ＣＧＨ２つで正方形を作って考える
ＣＨが６cmになるので、ＢＣは１０cm
三角形ＣＧＨもう一つ用意して、斜めの辺同士がくっつくようにつなげると正方形ができます。この正方形の面積は３６c㎡です。だから、正方形の一辺ＣＨは６cmです。
ＢＣの長さは、１０cmになります。
３.（２）ＤＥ：ＥＦ：ＦＢの長さの比を求める
２つの「ちょうちょ」の形の相似な三角形を使ってＤＥ：ＥＢ、ＤＦ：ＦＢの比を求め、その比を合わせる
三角形ＥＧＤとＥＡＢは「ちょうちょ」の形の相似な三角形で、ＧＤが１０cm、ＡＢが１６cmなので、ＤＥとＥＢの長さの比は
：
です。同じように考えて、ＤＦとＦＢの長さの比は
：になります。
４.ＤＢの長さを使って、丸数字と四角の数字を会わせて求める
ＤＢの長さは、丸数字では
、四角の数字では
。どちらも同じ長さなので、丸数字は２倍、四角の数字は１３倍して数字を合せます。
それを使って、ＤＥ：ＥＦ：ＦＢの比は、１０：３：１３。
５.（３）四角形ＥＦＣＧの面積を求める
三角形ＡＣＧの面積から三角形ＡＦＥの面積を引く
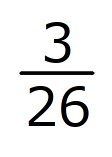倍の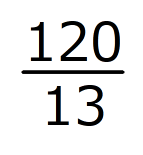
c㎡です。四角形ＥＦＣＧの面積は、８０からこれを引いて、
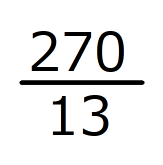c㎡になります。
