〔７〕相似図形の長さ・面積（過去問題）
（図）
（類題の問題）
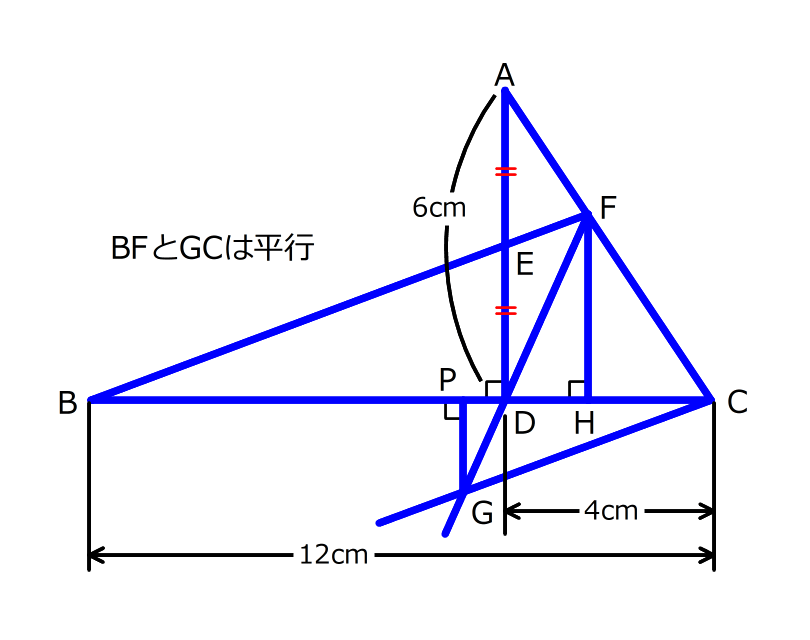
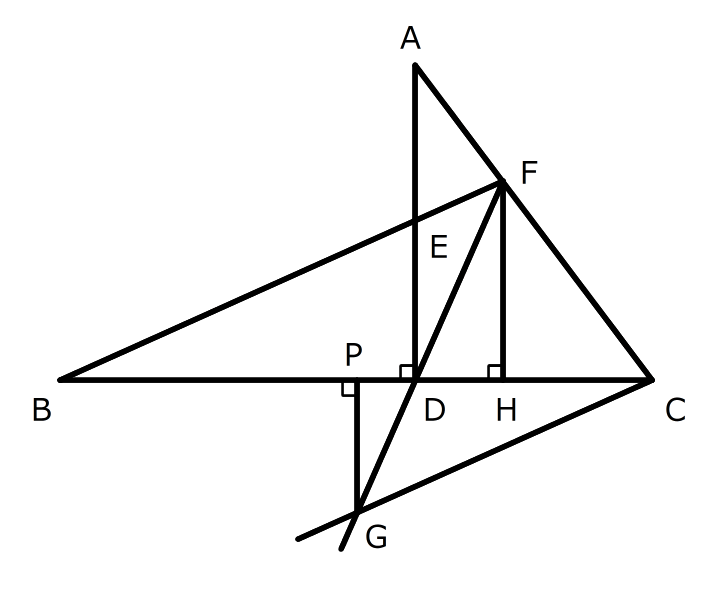図で、ＢＣ＝１５ｃｍ、ＤＣ＝６ｃｍ、ＡＤ＝８ｃｍ、角ＡＤＣ＝９０°です。ＡＤの中点をＥ、ＢＥを延ばした線とＡＣの交点をＦとします。また、ＦからＢＣに垂直な線を引いて、交点をＨとします。次の問いに答えなさい。（１）ＢＨ：ＦＨを最も簡単な整数の比で答えなさい。
（２）三角形ＦＢＣの面積を求めなさい。
（３）Ｃを通り、ＢＦに平行な直線と直線ＦＤの交点をＧとします。また、ＧからＢＣに垂直な線を引いて、交点をＰとします。このとき、ＧＰの長さを求めなさい。
類題は こちら
（１）ＢＨ：ＦＨの比を求める
１.三角形ＢＥＤとＢＦＨが相似あることを使う
ＡＤとＦＨが平行なので、三角形ＢＥＤとＢＦＨは山の形の相似な三角形です。だから、ＢＤ：ＥＤの比とＢＨ：ＦＨの比は同じになります。
長さを書き込むとＢＤ：ＥＤが８：３だと分かるので、ＢＨ：ＦＨも８：３になります。
（２）三角形ＦＢＣの面積を求める
２．もう一つ相似な三角形を考えることで、ＦＨの長さを求める
点Ｃの方から同じように考えると、三角形ＣＡＤとＣＦＨが相似で、ＣＨ：ＦＨ＝２：３だと分かります。「１」の場合も今度の場合も、ＦＨを表す比は３で同じなので、ＢＣを表す比が１０だと分かります。ＢＣの長さは１２センチなので、比１の長さは１.２センチになります。
ＦＨの長さはその３倍の３.６センチなので、三角形ＦＢＣの面積を計算することができます。
（３）ＧＰの長さを求める
３．三角形ＢＤＦとＣＤＧ、三角形ＦＤＨとＧＤＰの２つの相似を考えて、ＦＨとＧＰの比を求める
