〔7〕相似図形の長さ・面積(類題1)
(過去問題の図)
過去問題は
こちら
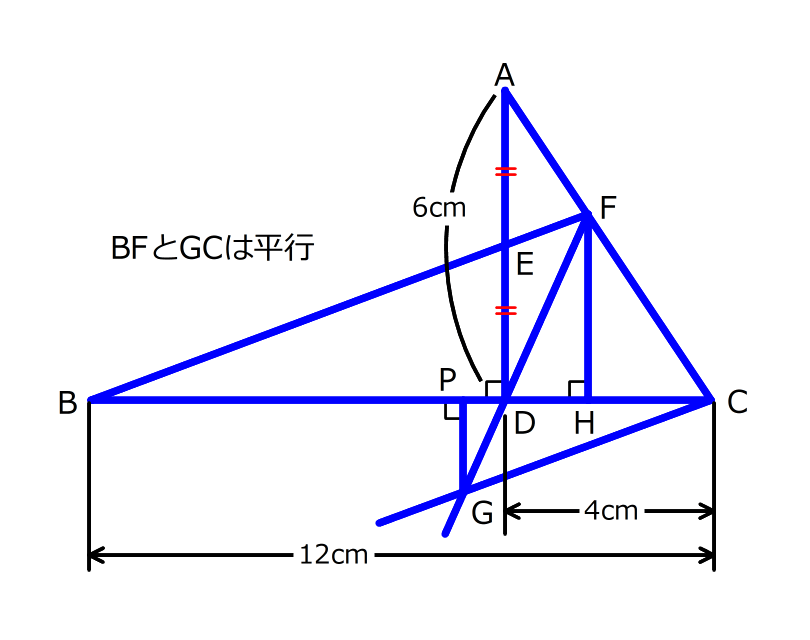
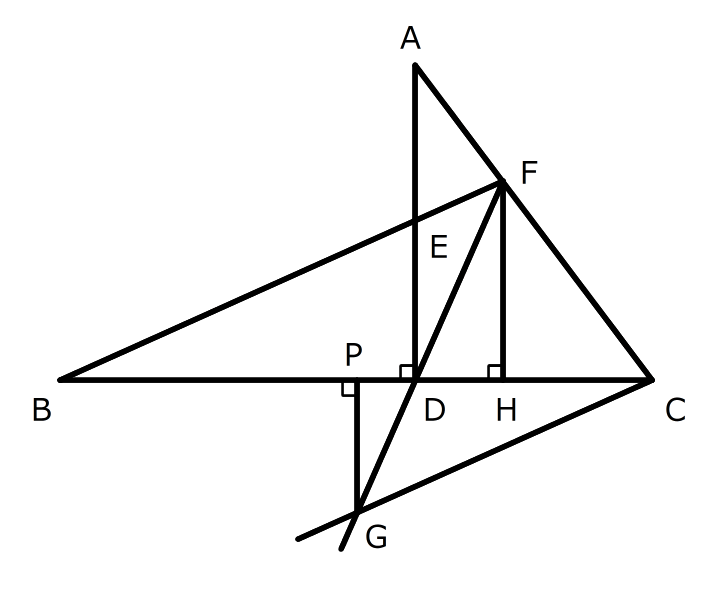
(1)BH:FHの比を求める
1.三角形BEDとBFHが相似あることを使う
ADとFHが平行なので、三角形BEDとBFHは山の形の相似な三角形です。だから、BD:EDの比とBH:FHの比は同じになります。
長さを書き込むとBD:EDが9:4だと分かるので、BH:FHも9:4になります。
(2)三角形FBCの面積を求める
2.もう一つ相似な三角形を考えることで、FHの長さを求める
点Cの方から同じように考えると、三角形CADとCFHが相似で、CH:FH=3:4だと分かります。「1」の場合も今度の場合も、FHを表す比は4で同じなので、BCを表す比が12だと分かります。BCの長さは15センチなので、比1の長さは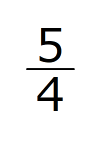 センチになります。
センチになります。
FHの長さはその4倍の5センチなので、三角形FBCの面積を計算することができます。
(3)GPの長さを求める
3.三角形BDFとCDG、三角形FDHとGDPの2つの相似を考えて、FHとGPの比を求める
BFとCGが平行なので、三角形BDFとCDGちょうちょの形の相似になります。BD:CD=3:2なので、FD:GDも3:2です。
FHとGPが平行なので、三角形FDHとGDPもちょうちょの形の相似です。FD:GD=3:2なので、FH:GPも3:2です。
つまり、PGはFHの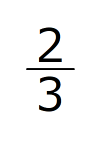 の長さで、
の長さで、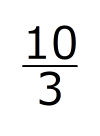 センチです。
センチです。





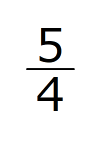 センチになります。
センチになります。


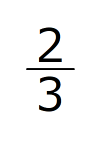 の長さで、
の長さで、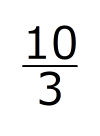 センチです。
センチです。

