〔3〕台形の面積(類題1)

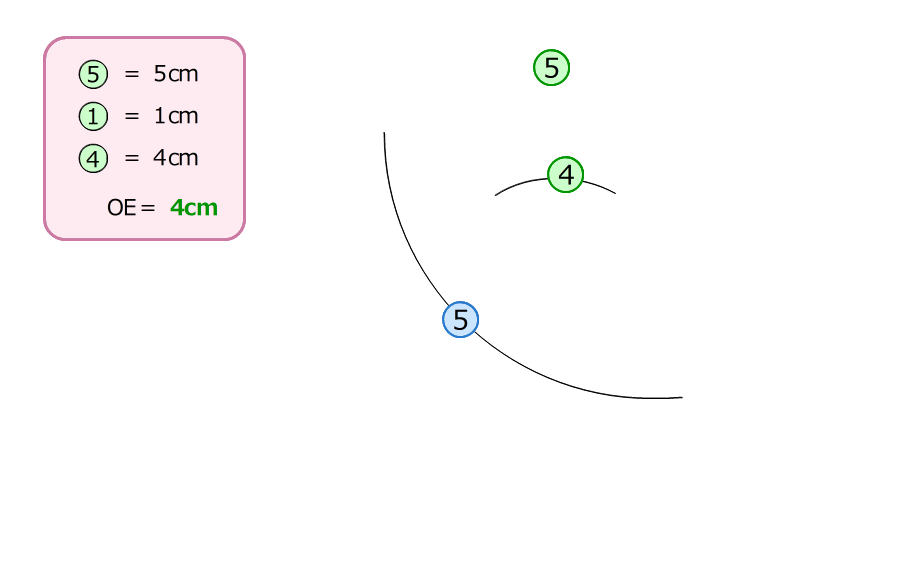
(1)辺OEの長さを求める
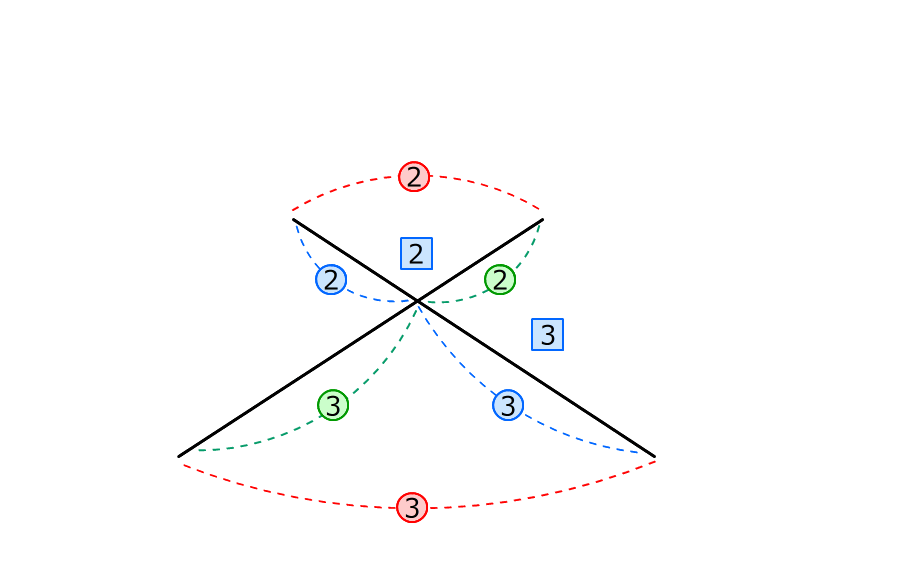
1.三角形OADと三角形OCBは、ちょうちょの形の相似
ADが5センチ、BCが20センチなので、2つの三角形の長さの比は1:4
2.三角形COEと三角形CADは山の形の相似
長さの比は4:5
⑤のADが5センチなので、④のOEは4センチ
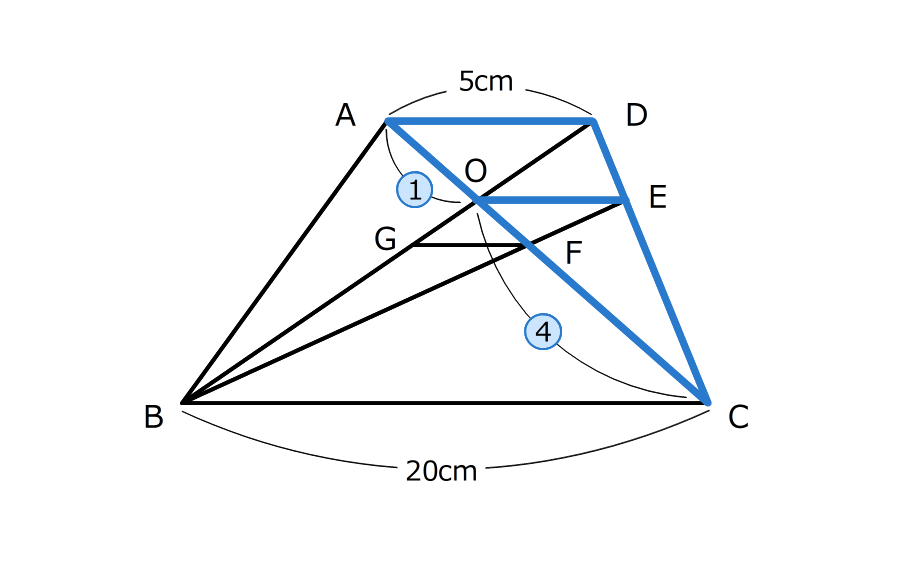

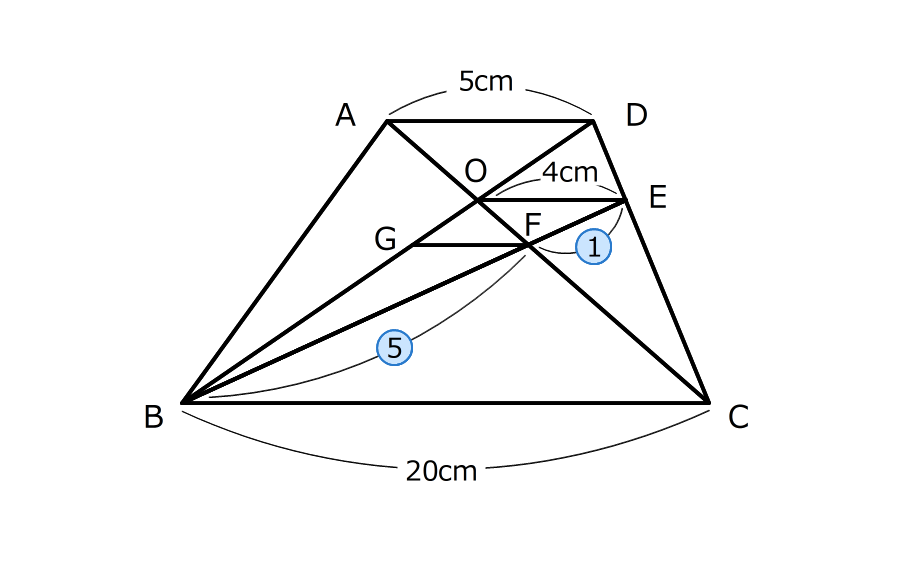
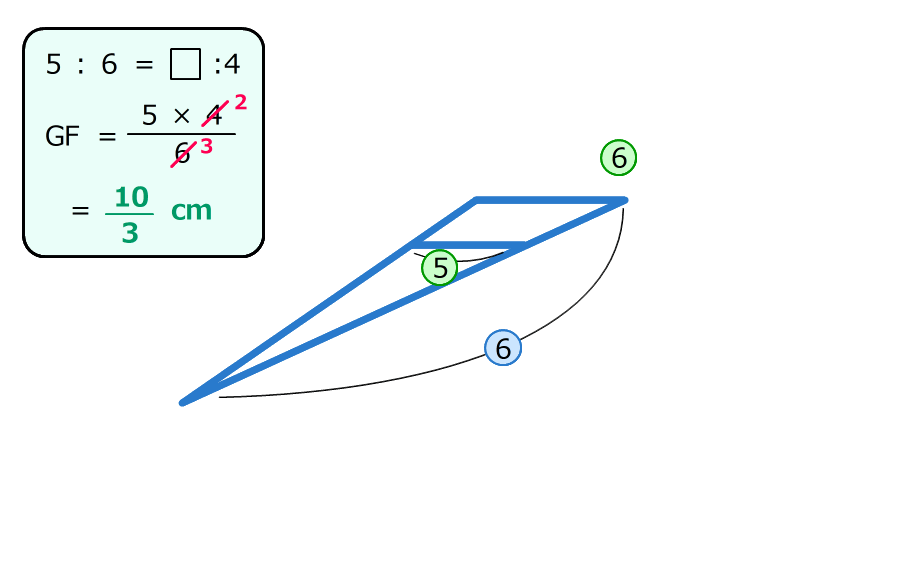
(2)辺GFの長さを求める
3.三角形FOEと三角形FCBは、ちょうちょの形の相似
OEが4センチ、BCが20センチなので、2つの三角形の長さの比は1:5
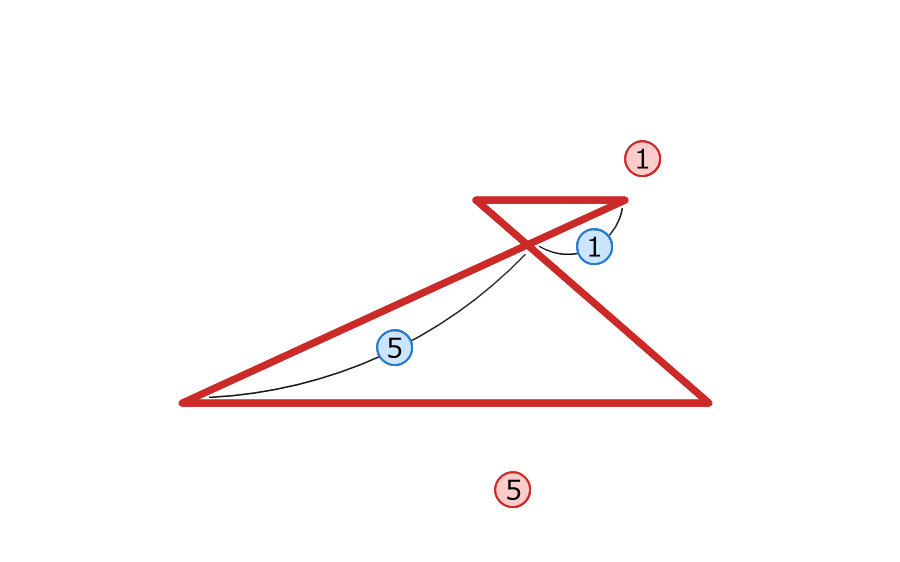

4.三角形BFGと三角形BEOは山の形の相似
長さの比は5:6
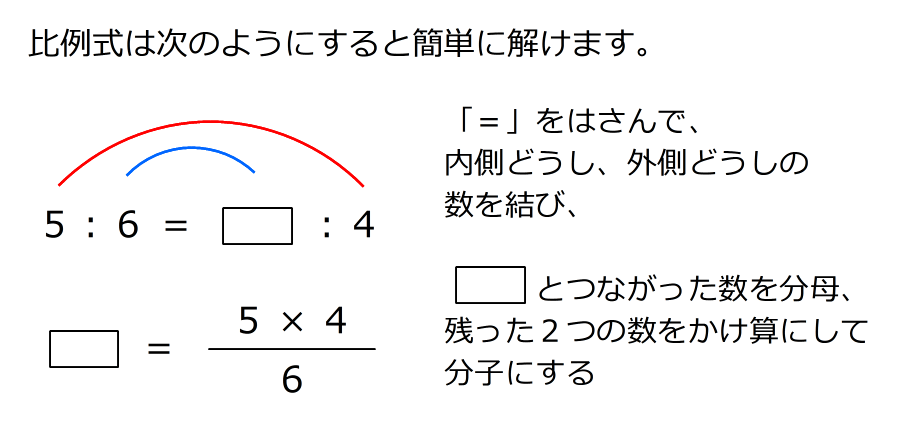
5:6=□:4cmの比例式を解いて求める


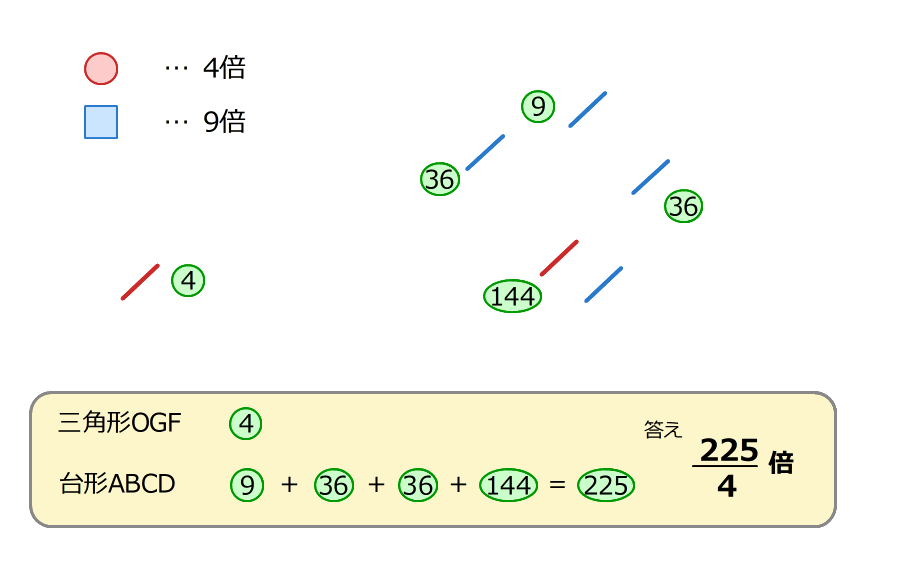
(3)台形ABCDの面積が、三角形OGFの面積の何倍か求める
5.山の形の相似を考えて、三角形OGFと三角形OBCの面積の比は :
:
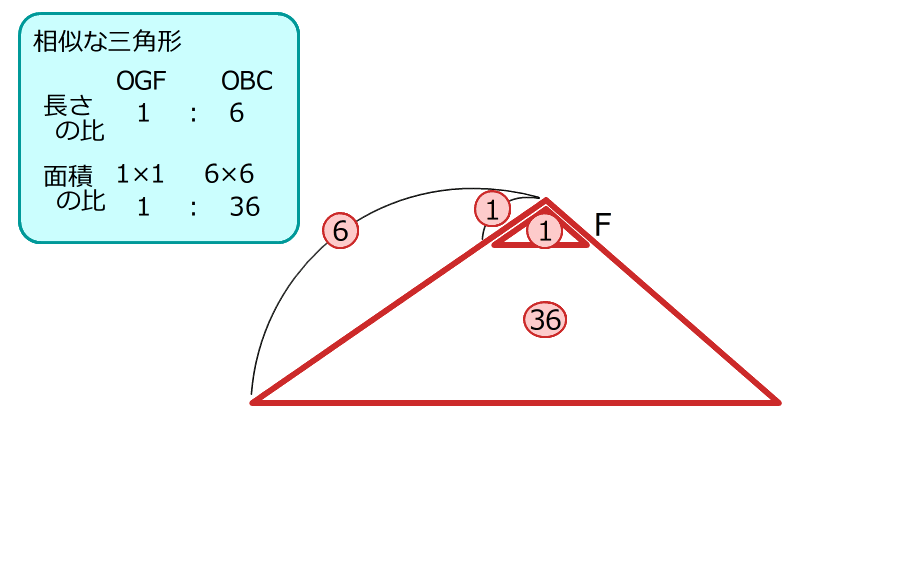

山の形の相似な三角形の面積の比は、辺の長さを2回ずつかけた数を使って簡単に表すことができます。
よく使うので、覚えておくと便利です。
理由は、下の「8.」「9.」を見てください。
今すぐ見るなら こちら
よく使うので、覚えておくと便利です。
理由は、下の「8.」「9.」を見てください。
今すぐ見るなら こちら

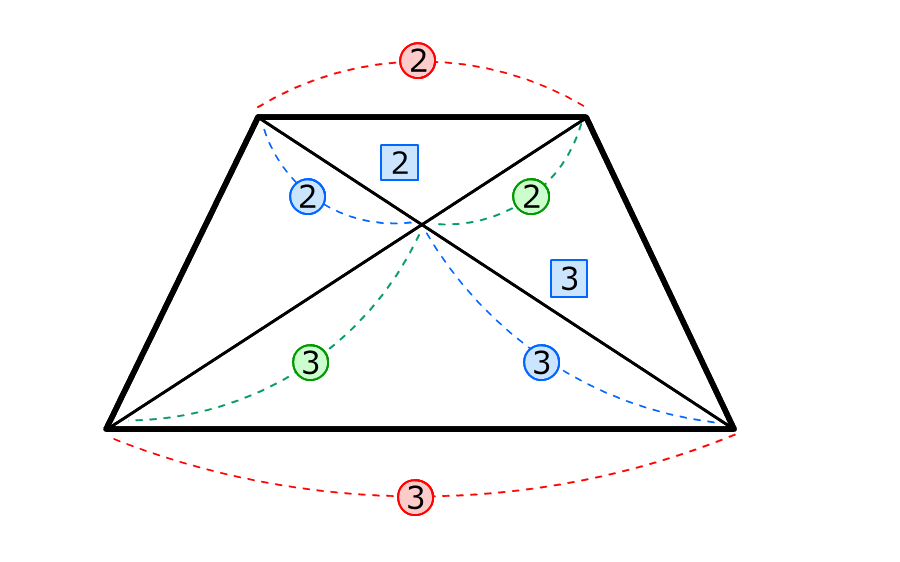
6.台形ABCDを対角線で4つに割る
4つの三角形の面積の比は :
: :
: :
:
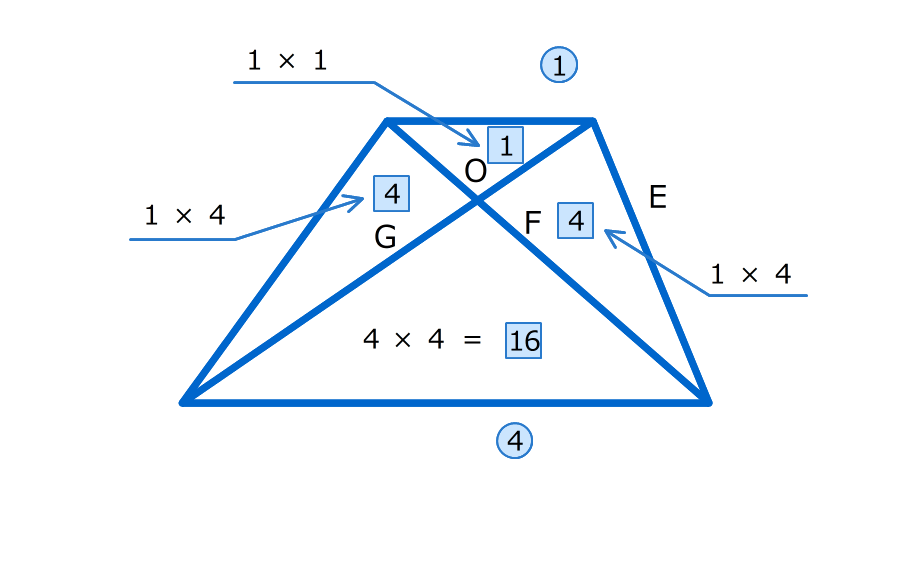

台形に対角線を引いてできる4つの三角形の面積の比は、上底と下底の長さの比を使って簡単に求めることができます。
よく使うので、覚えておくと便利です。
理由は、下の「10.」「11.」を見てください。
今すぐ見るなら、 こちら
よく使うので、覚えておくと便利です。
理由は、下の「10.」「11.」を見てください。
今すぐ見るなら、 こちら

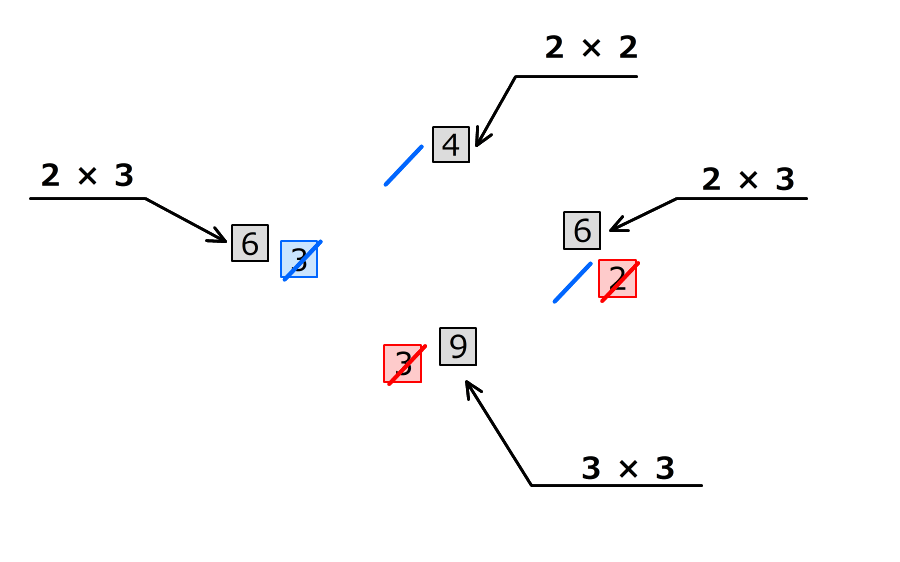
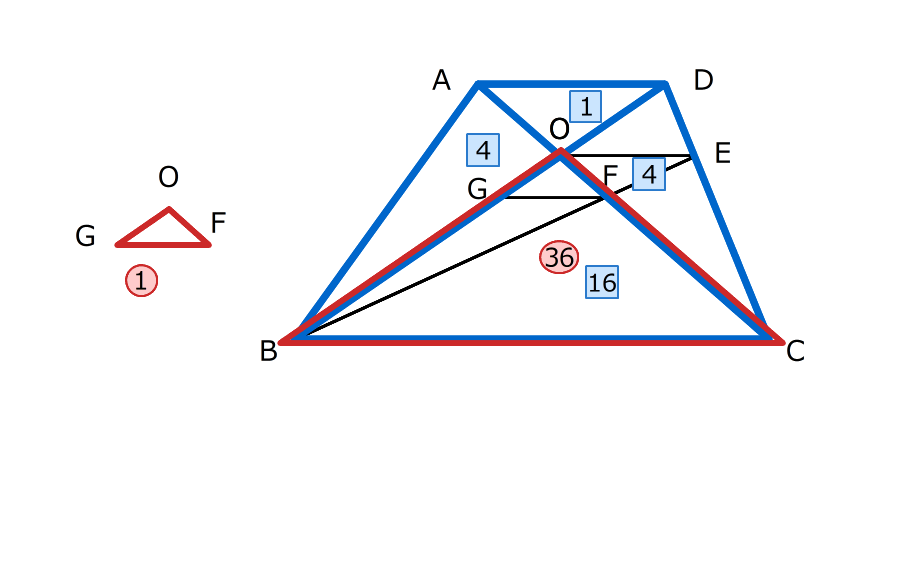
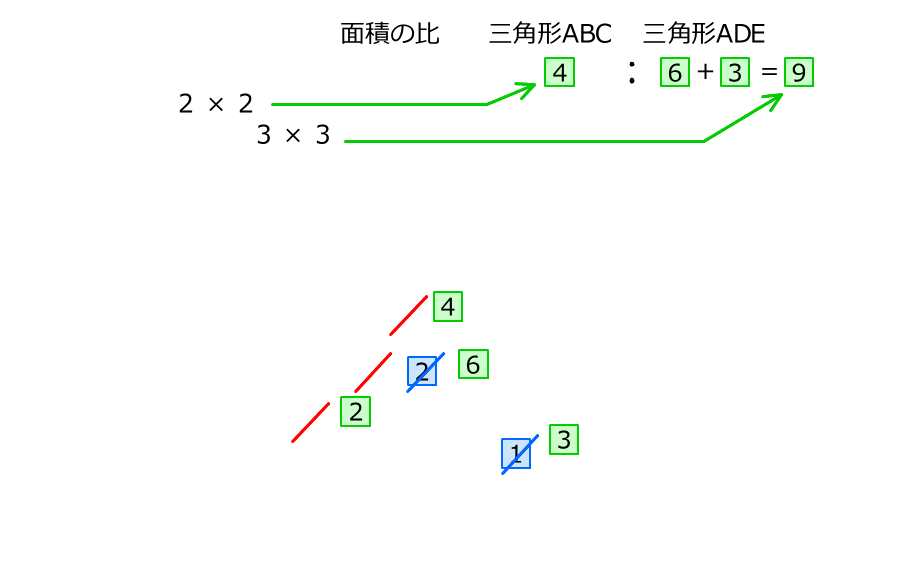
7.三角形OBCの面積から、丸数字を4倍し、四角の数字を9倍する
三角形OFGの面積は 、台形ABCDの面積は
、台形ABCDの面積は

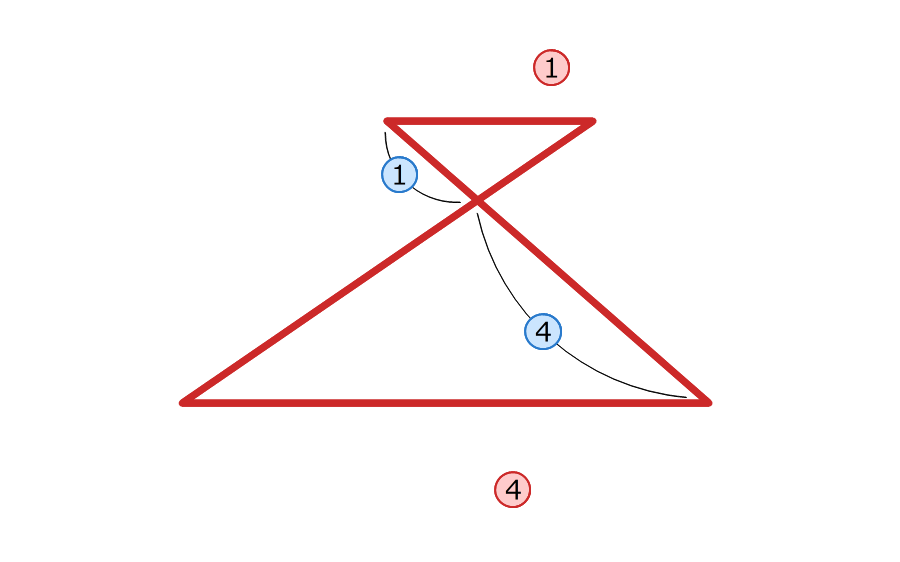
(理由1)山の形の三角形の面積の比
8.① 点DとCをつなぐと、三角形ABCと三角形CBDの面積の比は2:1になる
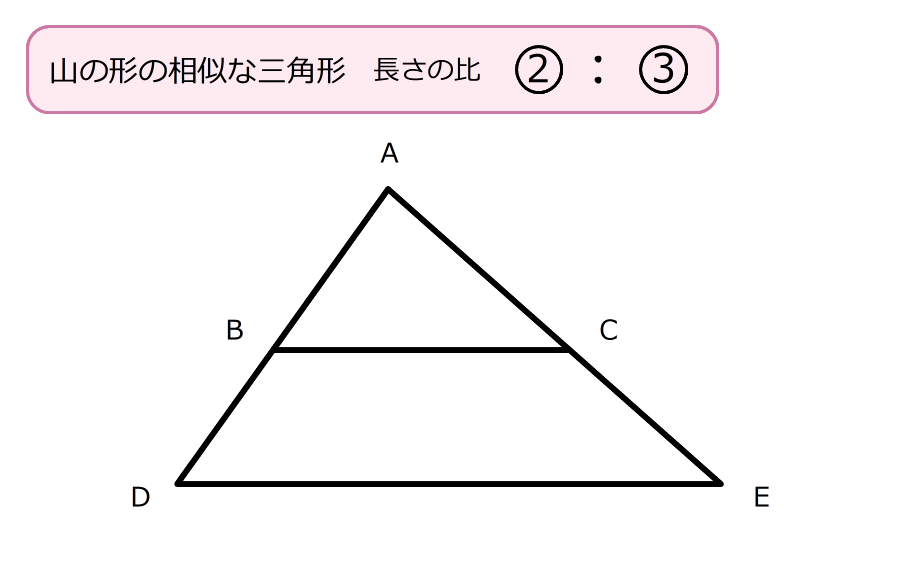
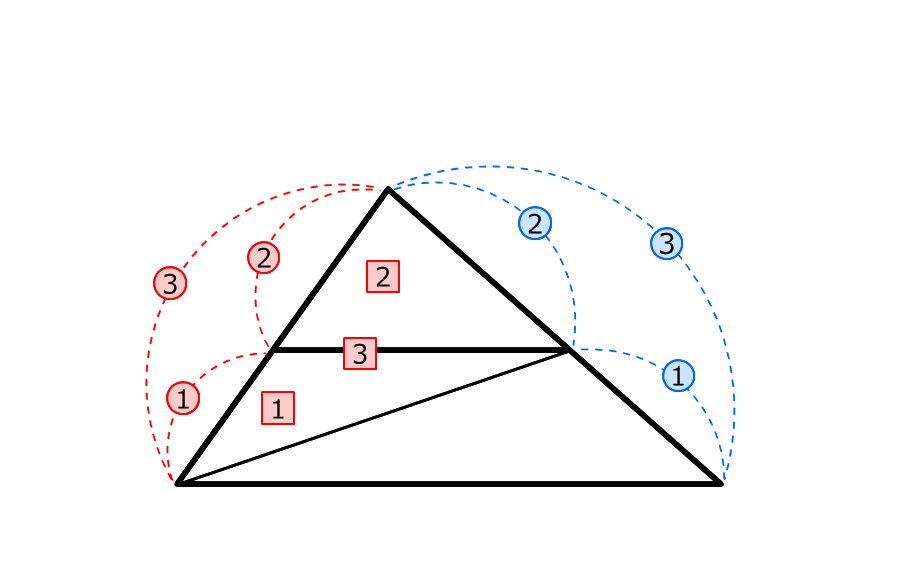

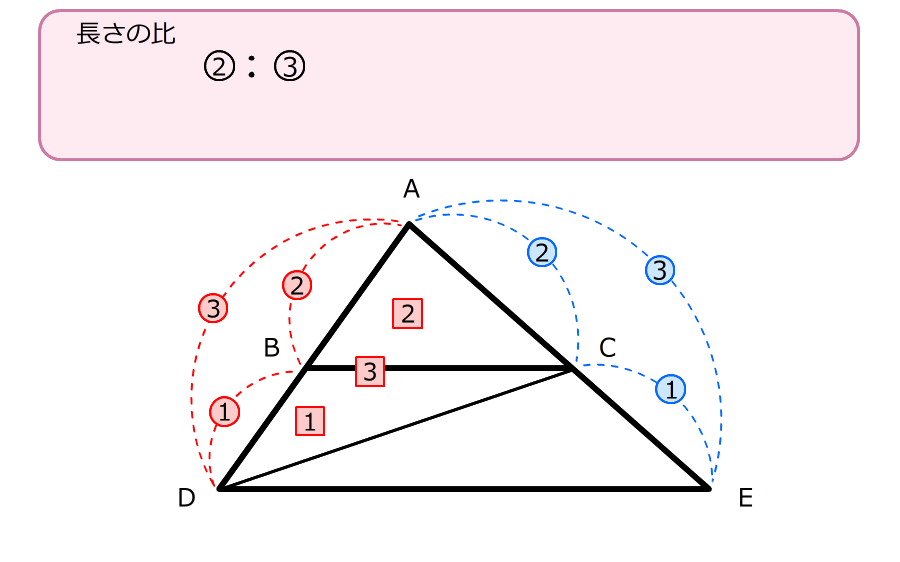
9.② 三角形ADCと三角形CDEの面積の比は、2:1になる
三角形ADCの面積は、赤い四角では3、青い四角では2なので、数字を合わせる
三角形ABCと三角形ADEの面積の比は4:9になって、長さの比2:3の数字を2回ずつかけた数字になっている

(理由2)台形の対角線を結んでできる4つの三角形の面積の比
10.① 高さが同じ2つの三角形の面積の比は、底辺の長さの比と同じことを使って、台形の中の右上側2つの三角形の面積の比を求める
青い四角の数字で表す
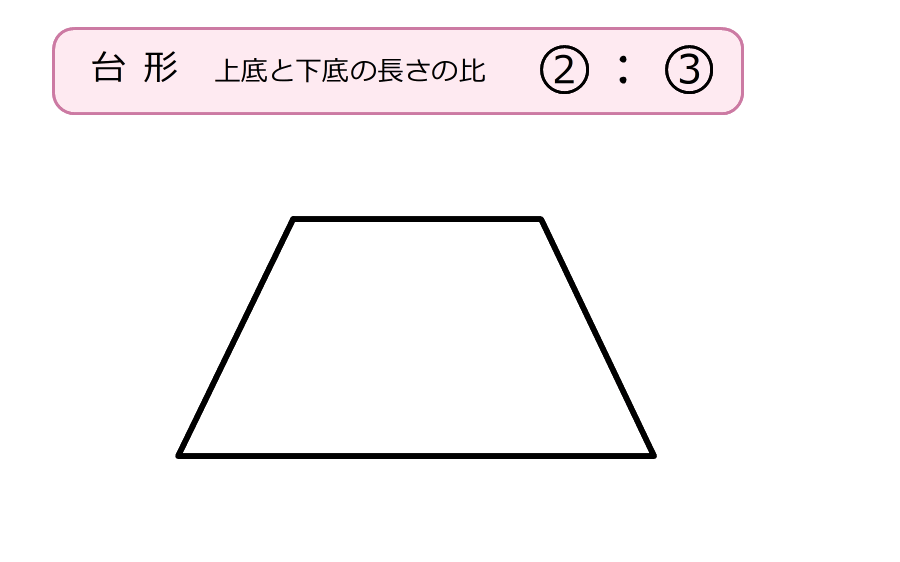

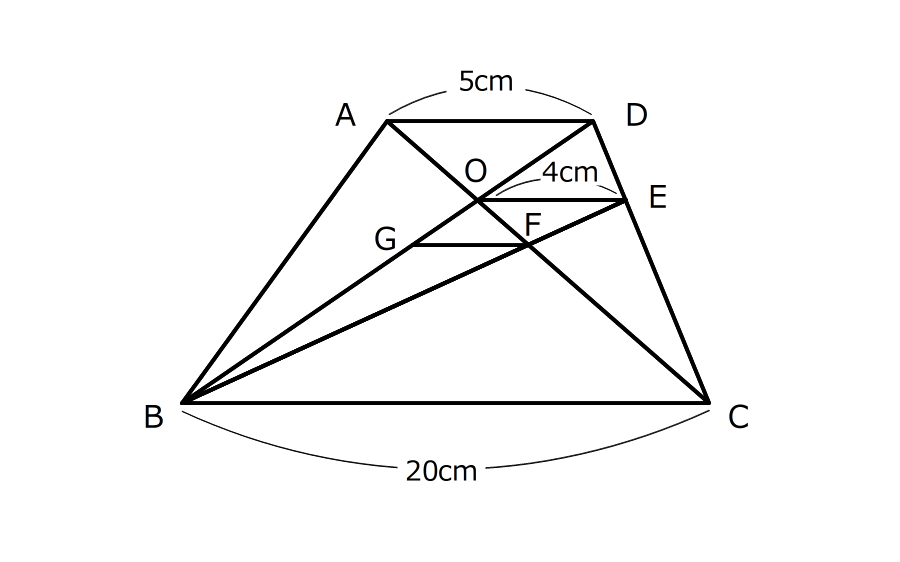
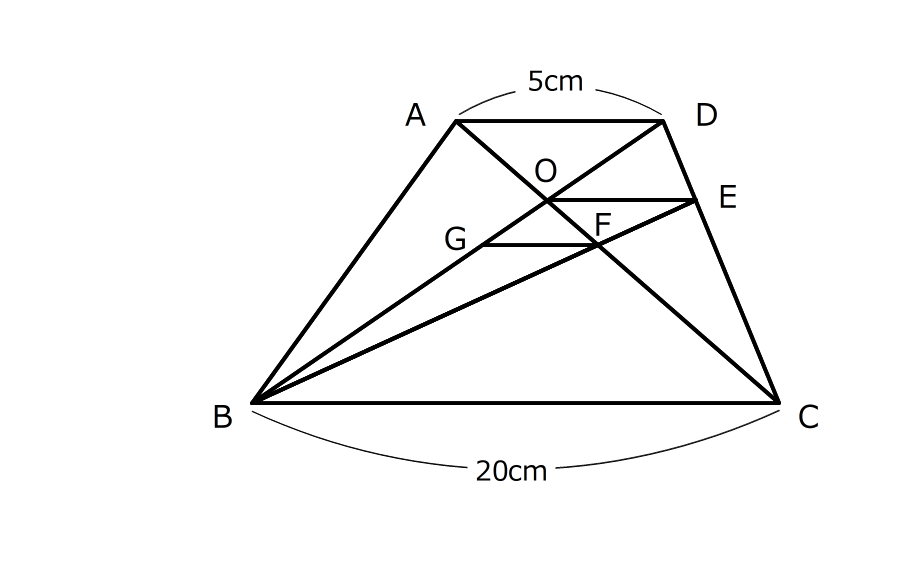
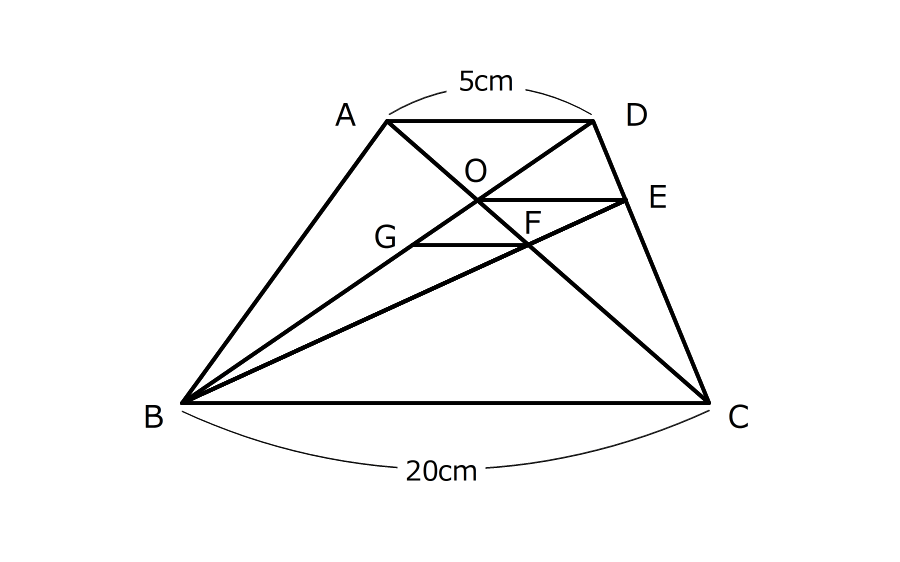
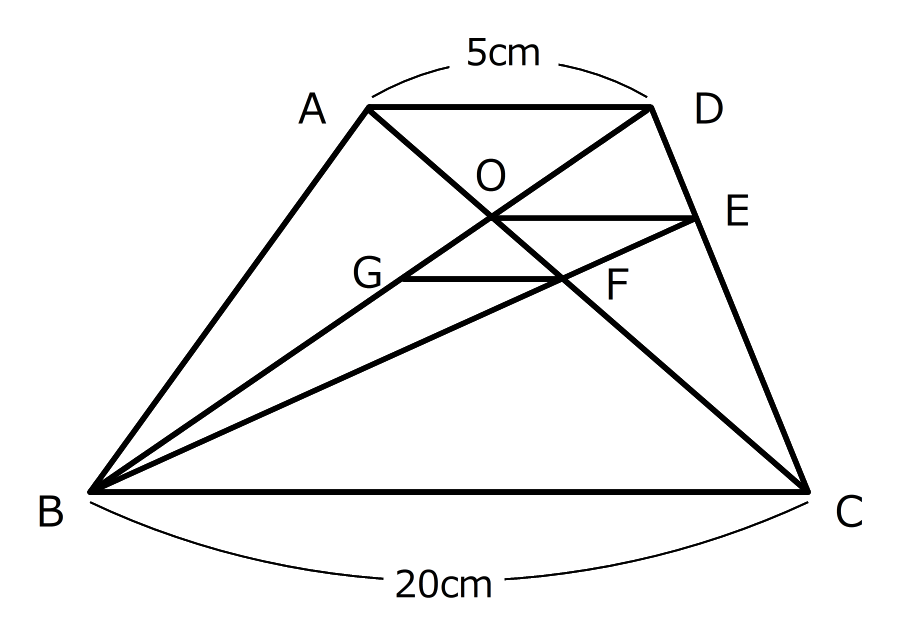 辺ADとBCが平行な台形ABCDがあります。対角線の交点Oを通って辺BCに平行な直線が辺DCと交わる点をEとします。さらに、EBとACが交わる点をFとし、Fを通ってBCに平行な直線がBDと交わる点をGとします。AD=5cm、BC=20cmのとき、次の問いに答えなさい。
辺ADとBCが平行な台形ABCDがあります。対角線の交点Oを通って辺BCに平行な直線が辺DCと交わる点をEとします。さらに、EBとACが交わる点をFとし、Fを通ってBCに平行な直線がBDと交わる点をGとします。AD=5cm、BC=20cmのとき、次の問いに答えなさい。