〔４〕速さ・連比（過去問題）
（図）
（類題の問題）
Ａさん、Ｂさん、Ｃさんの３人が同じ地点から同じ道を歩きます。Ａさんが出発してから５分後にＢさんが出発し、さらに５分後にＣさんが出発します。Ｂさんは出発してから２０分後にＡさんを追いぬきます。Ｃさんは出発してから２０分後にＢさんを追いぬきます。このとき、次の問いに答えなさい。
（１）Ａさん、Ｂさん、Ｃさんの歩く速さの比を最も簡単な整数の比で答えなさい。
（２）ＣさんがＡさんを追いぬくのは、Ｃさんが出発してから何分後ですか。
類題は こちら
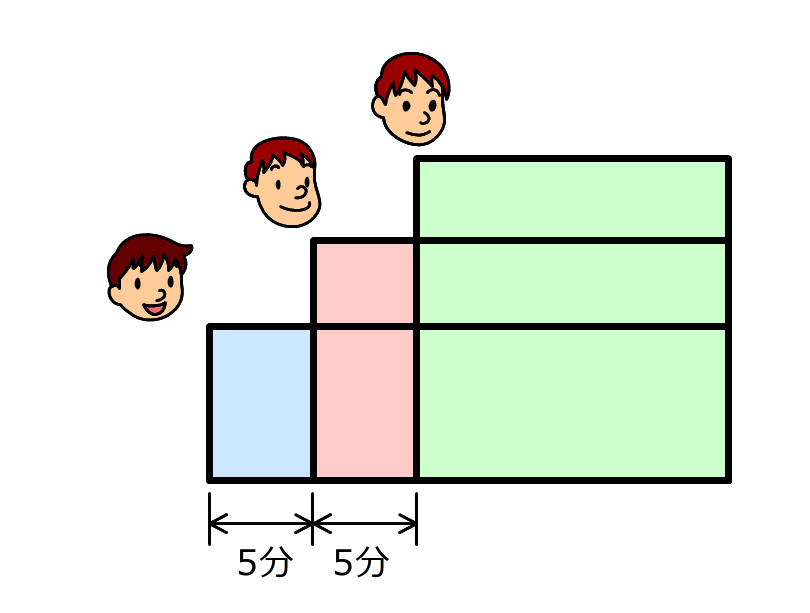
（１）Ａ君、Ｂ君、Ｃ君の歩く速さの比を求める
１．面積図を使って考える
Ａ君とＢ君の面積図を書きます。Ａ君が出発してから５分後に、Ｂ君は出発し、それから１５分後にＡ君を追いぬきます。このとき、二人が歩いた道のりは同じなので、二人の四角の面積は同じです。だから、それぞれの四角から、重なったところを除いた部分の面積も同じです。
面積が同じ四角の、縦と横の長さの比は逆比になります。時間の比が５：１５＝1：３であることから、Ａ君とＢ君の歩く速さの比がは３：４であることが分かります。
２．Ｂ君とＣ君の比も同じようにして求め、「１」で求めた比と合わせて、３人の歩く速さの比を求める
Ｂ君とＣ君の面積図を書くと、Ａ君とＢ君の場合と同じ絵になります。だから、Ｂ君とＣ君の歩く速さの比は、Ａ君とＢ君のときと同じで３：４になります。
Ａ君とＢ君の比と、Ｂ君とＣ君の比を、Ｂ君の数字が同じになるように合わせます。Ａ君、Ｂ君、Ｃ君の歩く速さの比は、９：１２：１６です。
（２）Ｃ君がＡ君を追いぬくのは、Ｃ君が出発してから何分後か求める
３．Ａ君とＣ君の面積図を書いて求める
が１０分なので、Ｃ君が出発してからＡ君を追いぬくまでの時間
は、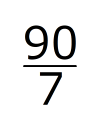
秒になります。
