〔7〕速さの問題(過去問題)
(図)
問題の確認
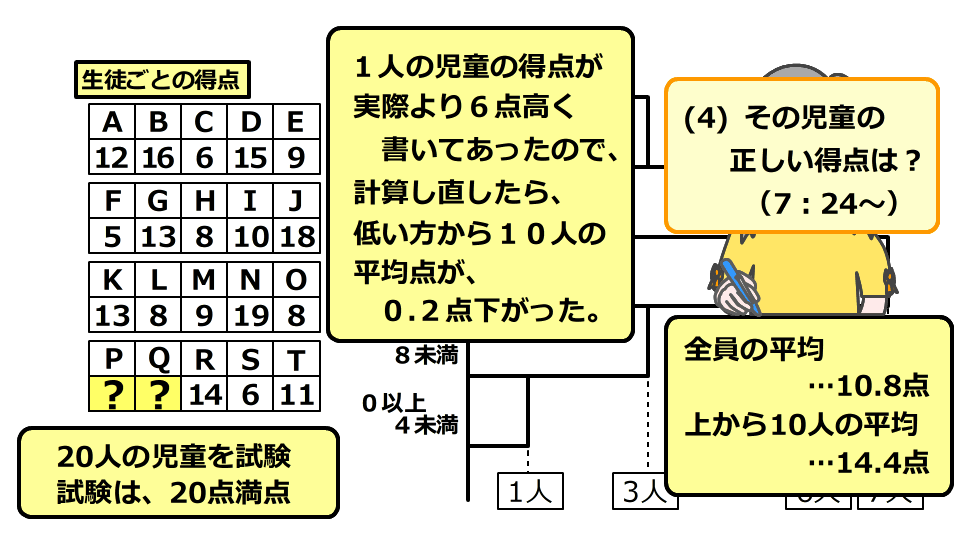
20の児童が20点満点のテストを受けました。結果は、点数の分からないPさん、Qさんを除いて表のとおりです。右のグラフはそれをまとめたものです。
全員の平均点が10.8点で、上の方10人の平均点は14.4点です。また、PさんとQさんでは、Pさんの点数の方が低いことが分かっています。
このとき、(1)PさんQさんがグラフのどこに入るか、 (2)Qさんの点数、(3)Pさんの点数、を求めます。
その後、一人の児童の点数が6点高くなっていたことが分かり、計算し直したら下の方10人の平均点が0.2点低くなりました。このとき、この児童の正しい点数を求めます。
1.(1)Pさん、Qさんが、グラフのどこに入るか求める
点数の分かっている児童を、グラフに書き込んで考える
点数の分かっている児童をグラフに書き込むと、グラフの上から2番目のところと、1番下のところが1人分ずつ空いていることが分かります。Pさんの点数の方がQさんの点数より低いので、Qさんは上から2番目、Pさんは1番下のところに入ります。だから答えは②です。
2.(2)Qさんの点数を求める
グラフの1番上に3人、2番目に6人の児童がいるので、3番目の7人のうち1番点数の高いTさんまでが、上から10人に入ります。
3.上から10人の平均点が分かっているので、上から10人の合計点を考える
上から10人の点数の平均点が14.4点なので、上から10人の合計点は144点になります。
上から10人の内、Qさんを除いた9人の合計点を計算すると131点になるので、Qさんの点数は13点です。
4.(3)Pさんの点数を求める
同じように、今度は下の10人の合計点を考える
20人全員の合計点は216点なので、下の10人の合計点は72点です。
下の10人の内、Pさんを除いた9人の合計点は69点なので、Pさんの点数は3点になります。
5.(4)6点高くなっていた児童の、正しく直された後の点数を求める
児童を上から10人、下から10人で分け、点数の順に並べて考える
点数が間違っていた児童が、正しく直す前と後で、上から10人下から10人のどちらのグループに入っているかで分けて考える。
① 上から10人にいた児童が、正しく直した後も上から10人のグループに入っていた場合、② 下から10人のグループに入っていた場合、の2つの場合には、下のグループの平均点が下がるのが0.2点にならないので条件に合いません。
条件に合うのは、正しく直す前は上のグループに入っていて、直した後は下から10人のグループに入る場合です。
5.1人の児童が上の10人のグループから下の10人のグループに移ると、下のグループにいる児童で1番点数の高い10点のIさんが上のグループに移る
このことから下のグループの平均点の変化を考える
Iさんが上のグループに移ると、下のグループの合計点は10点減ります。
実際には、下のグループの平均点は0.2点下がるので、合計点は2点減ったはずです。だから、上のグループから移ってきた児童の正しい点数は、10点と2点の差である8点のはずです。
この児童の、正しくする前の得点は6点を加えた14点なので、Rさんです。
だから、答えは8点になります。