〔2〕(8)正八面体の展開図(過去問題)
(図)
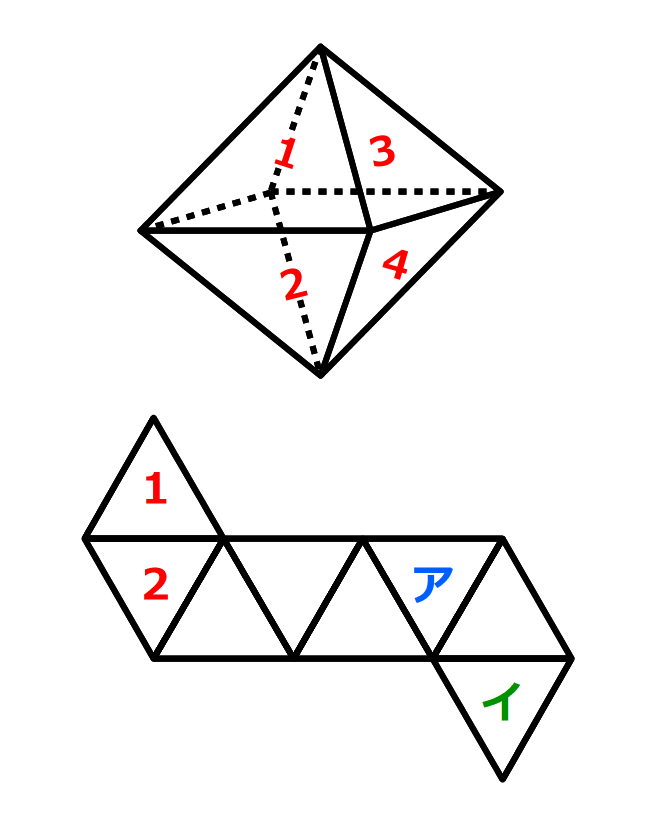

(類題の問題)
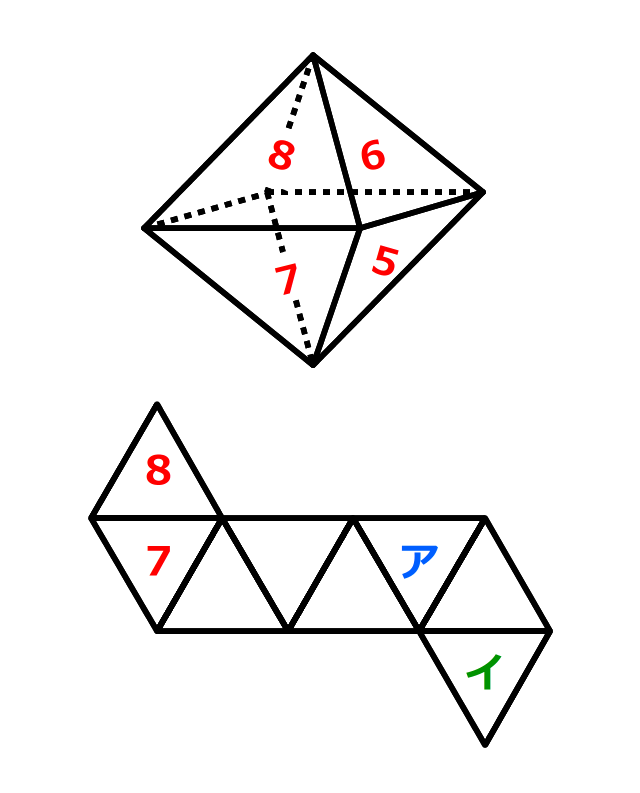
図のように、すべての面が同じ大きさの正三角形で、8つの面からなるサイコロがあります。サイコロの面の数字は、向かいあう平行な面の数字の和が9になるように配置されています。このとき、サイコロの展開図の面アと面イの位置にくる数字をそれぞれ答えなさい。
類題は こちら

1.「展開図でくぼんだところの両はしの点は、立体に組み立てたときくっつく」ことを使うと、「ア」の面の上側の辺が、「1」の面の左側の辺にくっつくことが分かる。
だから、「ア」の面は、「1」の面の左側で、「4」の面と向き合っている。

2.展開図で2のとなりの面は、4になる。
右下のくぼんだところを考えると、「イ」の面はその4の面の右側だと分かる。
4の右側の面は、1と向き合っているので8

3.(別解) 展開図で、2のとなりには4、そのとなりには3が入る。
「正八面体の展開図でまっすぐに並ぶ4つの面の、両はしの面同士は向き合っている」ことを使うと、3のとなりは2と向き合っているので7、アには5、そのとなりは6だと分かる。
イの面には、残った8が入る。




