〔6〕回転体の展開図(過去問題)
(図)

問題の確認
棒に三角形を張り付けて、その棒を回転させたときにできる立体があります。
できる立体は、円すい二つを、片方をひっくり返して底面同士をくっつけた形です。
(1)では、この立体の展開図を、与えられた図の中から選び、
(2)では、この立体の表面積を求めます。
1.(1)立体の展開図を考える
円すい2つを離して考える
円すいの展開図は、底面の円と側面のおうぎ形からできています。
立体は円すい2つからできていて、底面同士がくっついているので、底面はこの立体の展開図には含まれません。だから、この立体の展開図は、側面のおうぎ形2つをくっつけた形になります。
2.上と下のおうぎ形の中心角について考える
上のおうぎ形で考えます。底面の円の半径は1cmで、側面のおうぎ形を作っている円の半径は3cmです。だから、2つの円の円周の長さの比は1:3です。おうぎ形の弧と底面の円はくっつくので、おうぎ形は、おうぎ形を作っている円を3つに割った1つ分です。つまり、中心角は120度です。
下のおうぎ形も同じように考えると、おうぎ形の中心角は180度になります。
だから、答えはウです。
3.(2)立体の表面積を求める
上のおうぎ形は半径3cmの円の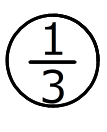 なので、面積は3×3.14です。下のおうぎ形は半径2cmの円の
なので、面積は3×3.14です。下のおうぎ形は半径2cmの円の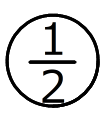 なので、面積は2×3.14です。
なので、面積は2×3.14です。
だから、立体の表面積は、5×3.14を計算して、15.7cm²になります。








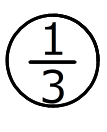 なので、面積は3×3.14です。下のおうぎ形は半径2cmの円の
なので、面積は3×3.14です。下のおうぎ形は半径2cmの円の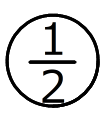 なので、面積は2×3.14です。
なので、面積は2×3.14です。