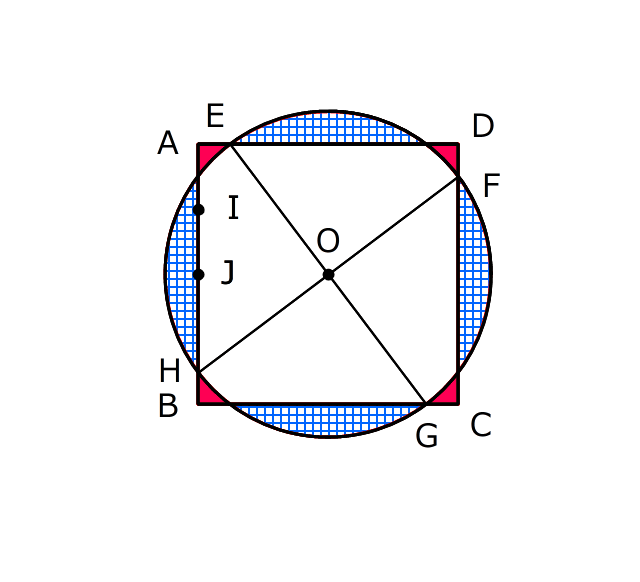
〔8〕正方形と円(面積・角度)(類題1)
(過去問の図)
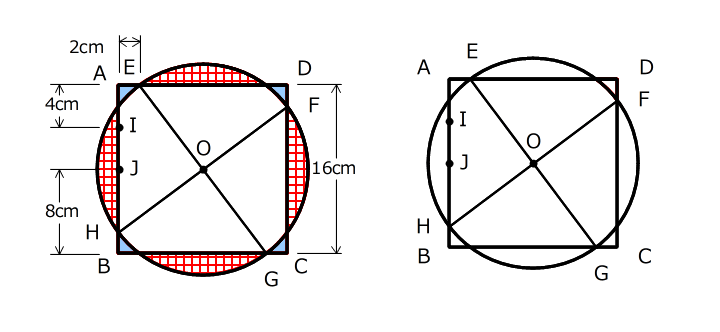
過去問題は
こちら
(1)円の半径を求める
1.三角形EHOの面積は、正方形の面積の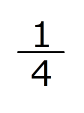 から三角形AHEの面積を引いて、12.5cm²。
から三角形AHEの面積を引いて、12.5cm²。
2.三角形EHOは直角二等辺三角形なので、EHの側にもう一つくっつけると、面積が25cm²の正方形ができる。
この正方形は1辺の長さは円の半径と同じで、5cm。
(2)あみが付いた部分の面積の合計と、色の付いた部分の面積の合計との差を求める。
3.あみが付いた部分と色の付いた部分に、真ん中の白い部分を足すと、それぞれ円と正方形になる。
だから、円の面積から正方形の面積を引いて、14.5cm²。
(3)角EIJの大きさを求める。
4.三角形EAIと三角形IJOはどちらも直角三角形。
直角の両側の辺の比が、どちらの三角形も1:2なので、2つの三角形は相似の三角形。
5.角AEIと角AIEの和は90度で、角AEI角JIOは同じなので、三角形EIOも直角三角形になる。
三角形EAIと三角形IJOの長さの比は1:2なので、辺EIとIOの比も1:2。
だから、三角形EAI、IJO、EIOの3つの三角形はすべて相似。。
6.角EIA、IOJ、EOIは同じ。その2つ分、角EOJが54°なので、1つは27°
角EIJは180°からそれを引いて、153°


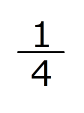 から三角形AHEの面積を引いて、12.5cm²。
から三角形AHEの面積を引いて、12.5cm²。