〔４〕じゃんけんゲーム（過去問題）

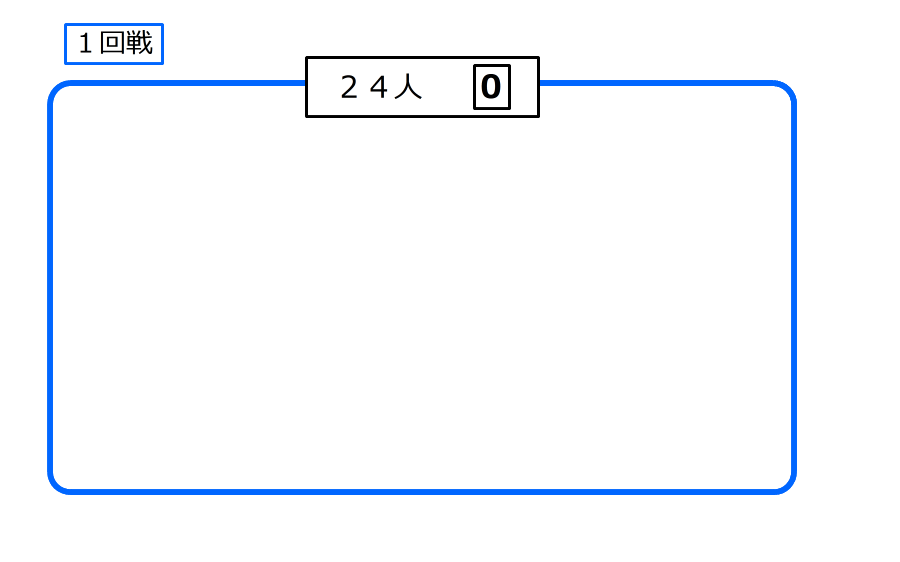
（１）２４人でゲームを始めて、３回戦が終わったときの結果を求める
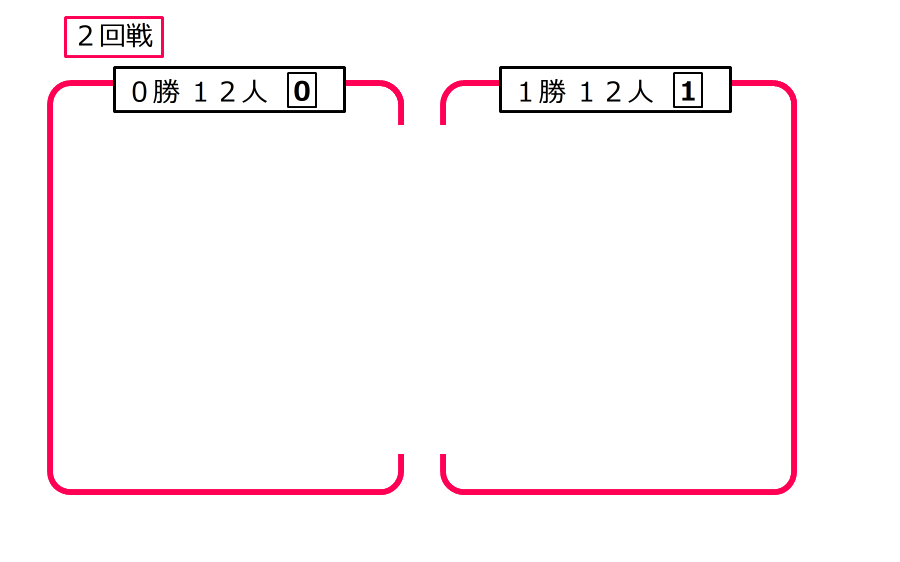
 １．１回戦でじゃんけんをすると、勝った１２人のカードは１になり、負けた12人のカードは０のまま

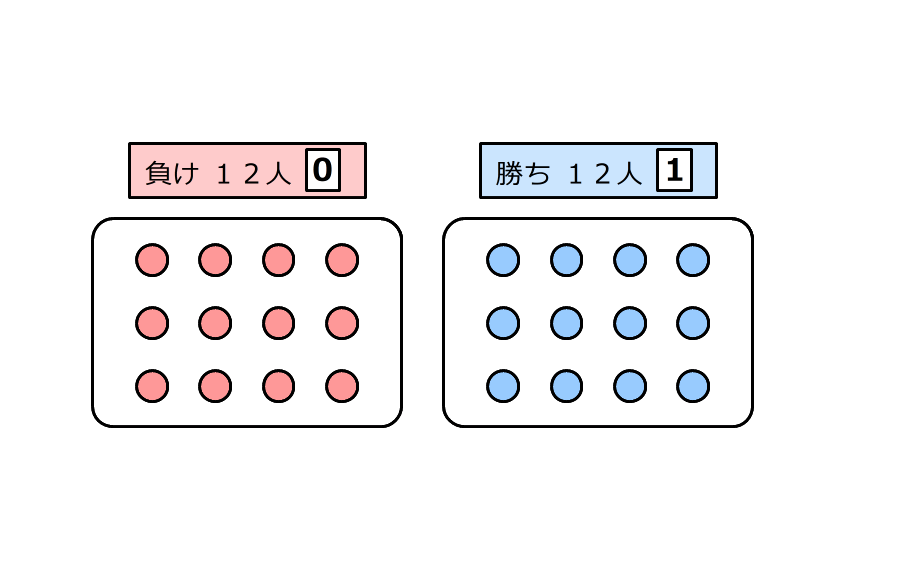
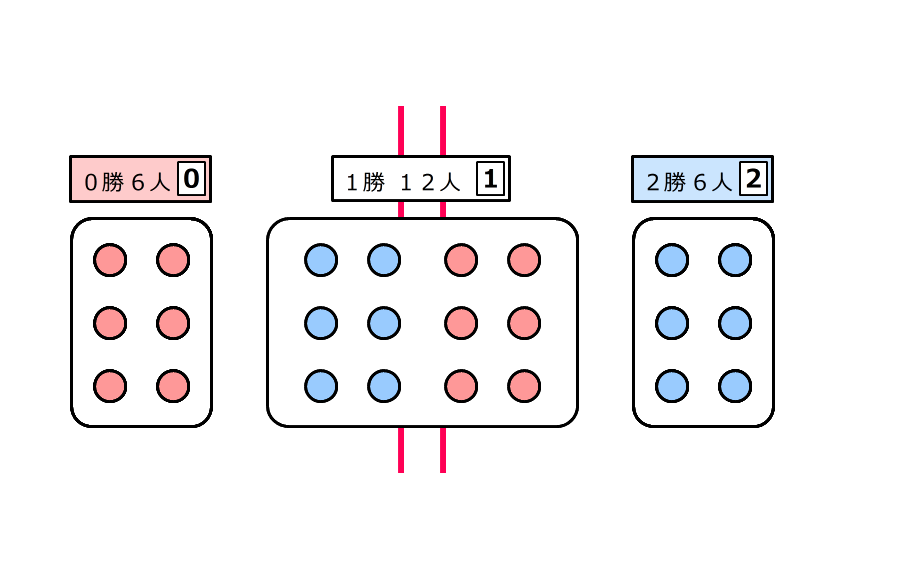
２．２回戦のじゃんけんのあと、２回続けて勝った人は６人で、カードは２
 １回目に勝って２回目は負けた人と、１回目に負けて２回目は勝った人は合わせて１２人、どちらも１勝なのでカードは１
 ２回続けて負けた人は６人でカードは０のまま

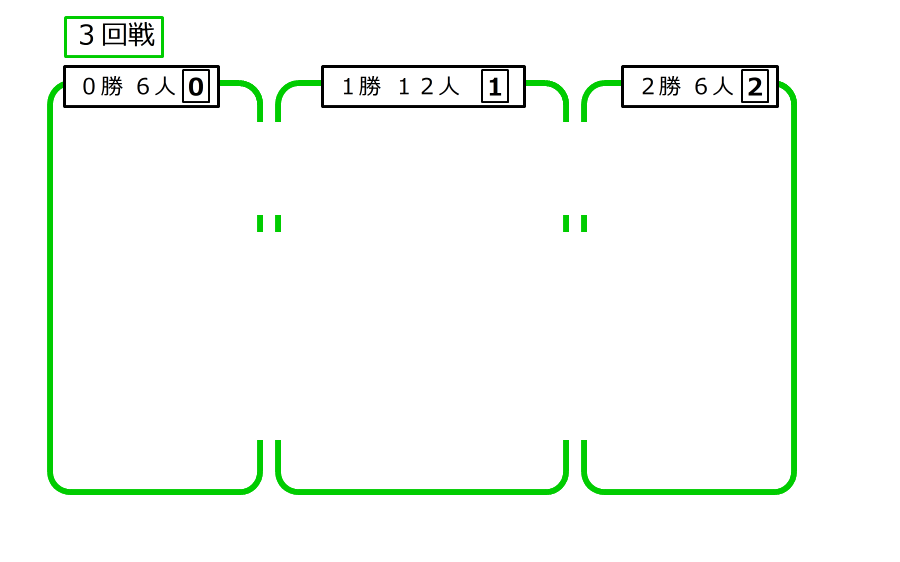
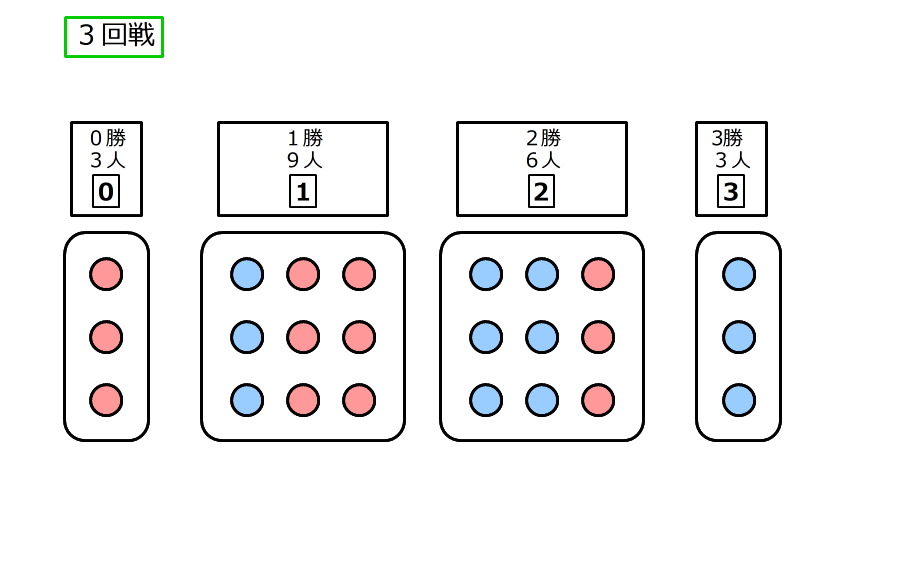
３．３回戦のじゃんけんの後、３回続けて勝った人は３人で、カードは３
 ２勝１敗と１勝２敗の人がそれぞれ９人で、カードは２と１
３回とも負けた人は３人で、カードは０

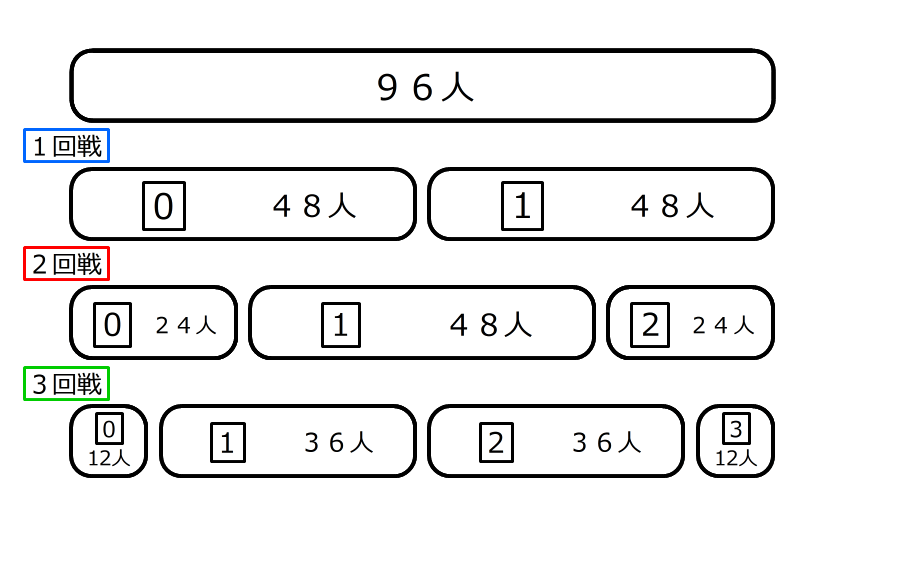
（２）９６人でゲームを行い、終わったときの結果を求める
 ４．勝ち続けの１番右側のグループ、負け続けの１番左側の人グループの人数は１回戦ごとに半分になる
 真ん中にグループにはカードの数が同じになるグループがあるので、いっしょになる

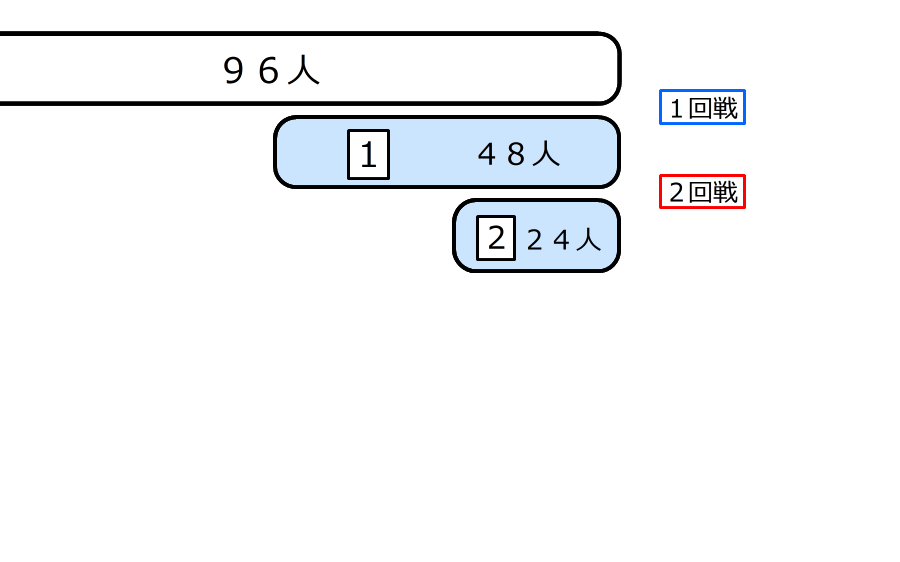
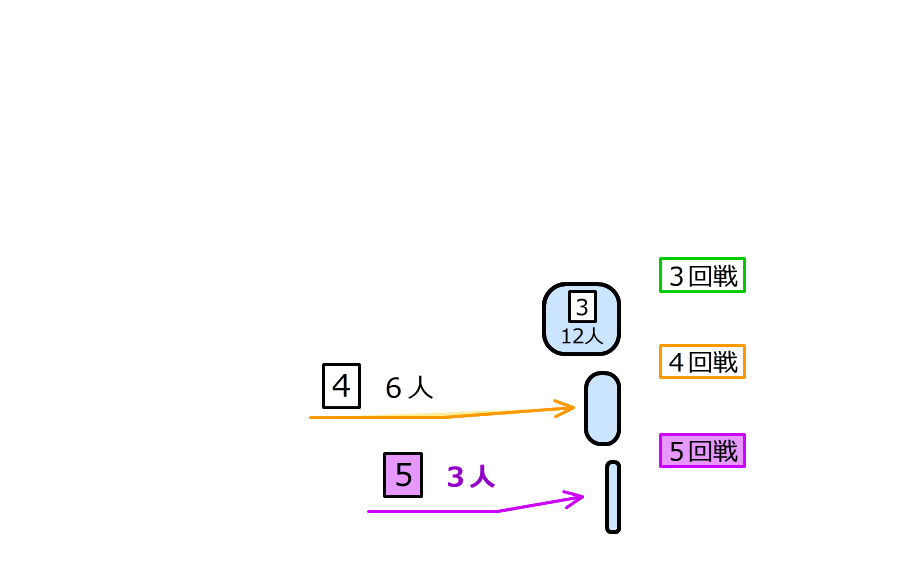
５．勝ち続けの一番右側のグループを考える
 ５回戦が終わったとき、グループの人数が３人になるのでゲームは終わる

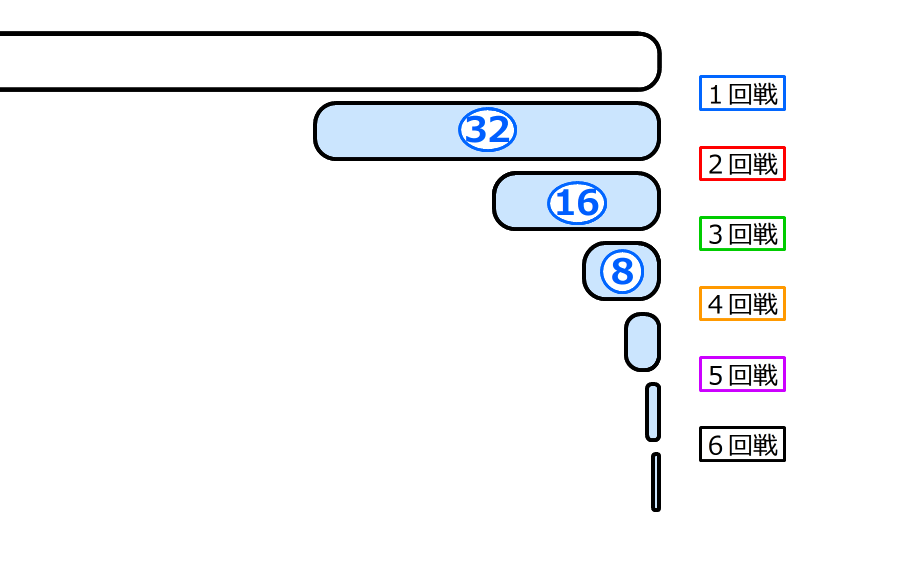
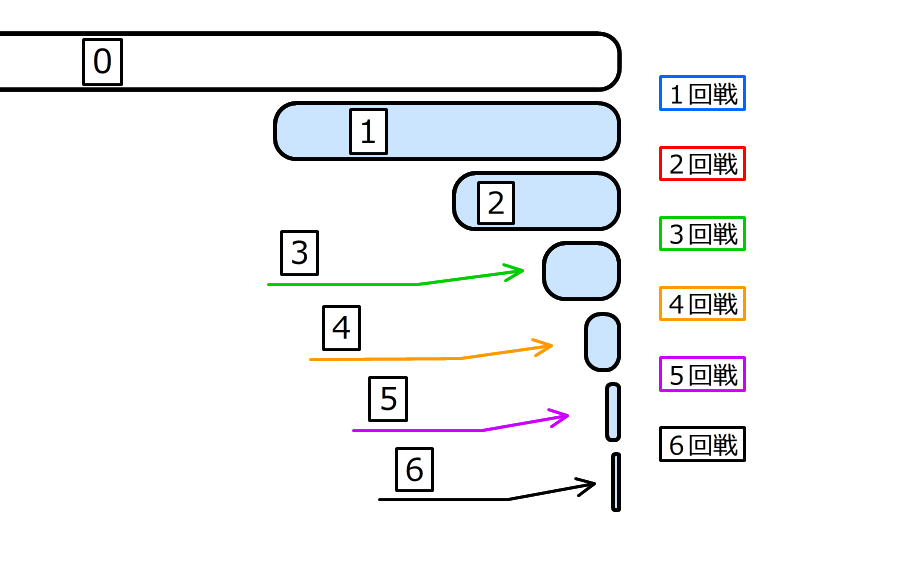
（３）６回戦でゲームが終了したとき、何人がゲームに参加したか求める
 ６．６回戦が終了したときの人数を①として、さかのぼって考える
 ①は奇き数で、１回戦さかのぼるごとに２倍になる

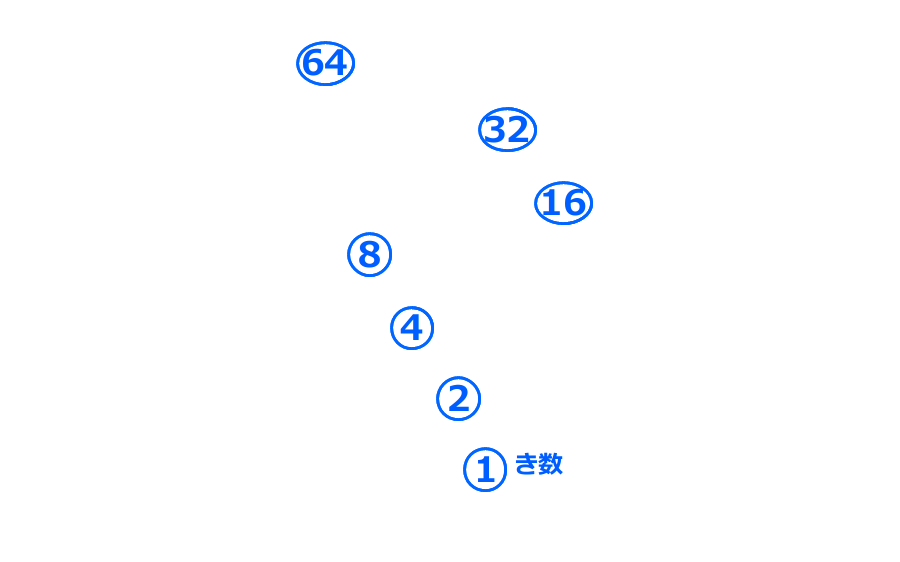
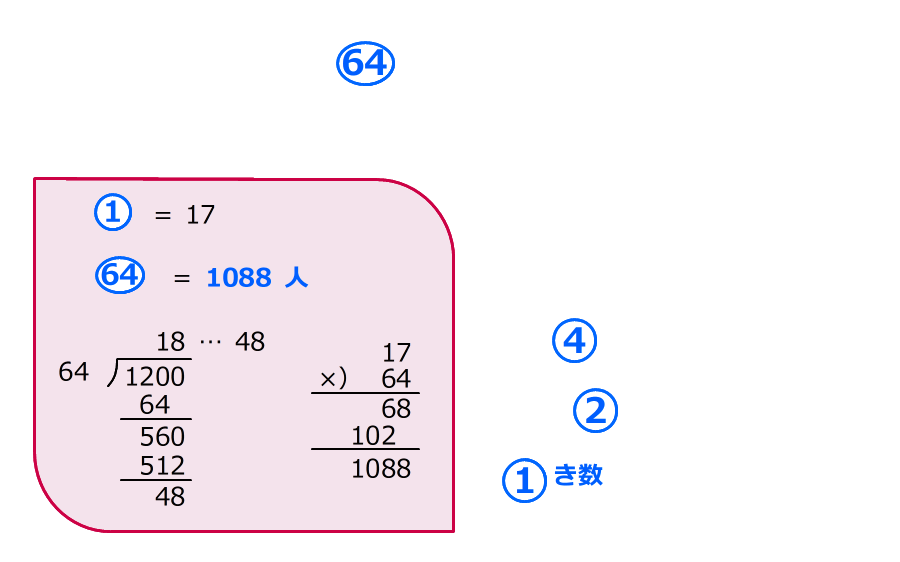
７．１２００以下で、が一番大きくなるような奇き数①を探さがす
 ①＝１７なので、ゲーム参加者の人数は１０８８人