〔５〕円柱の容積（過去問題）

（１）容器の表面積を求める
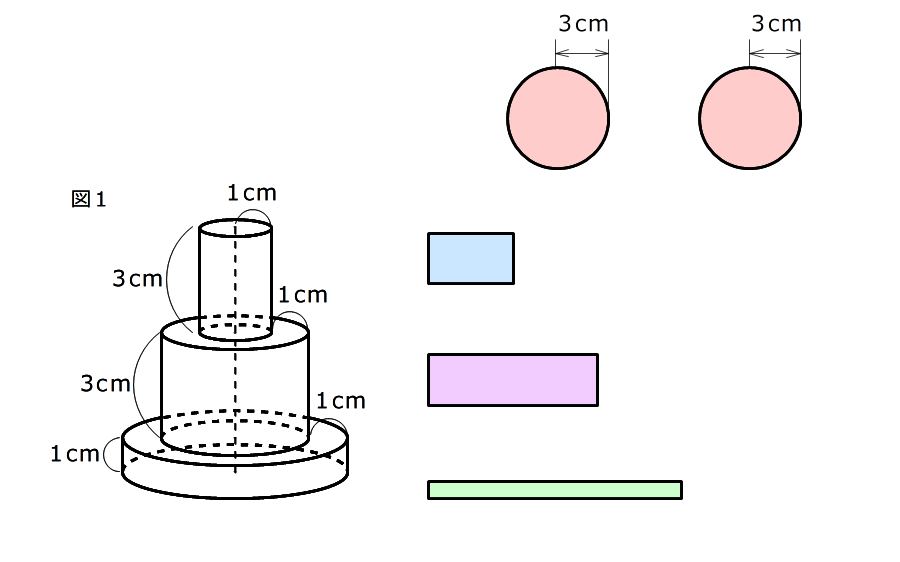
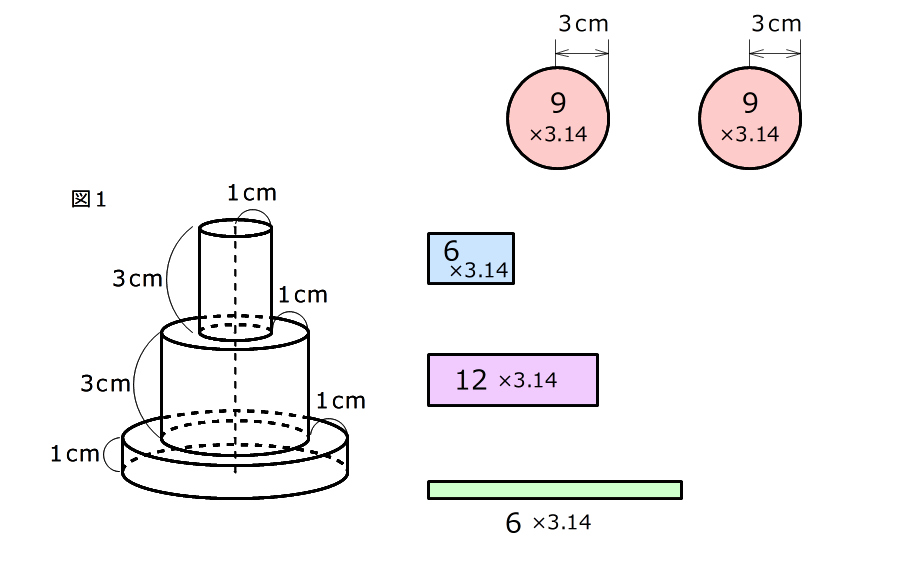
 １. 容器を、上から、下から、横から見たときに見える図形を書く
 円が２つと、長方形が３つできる

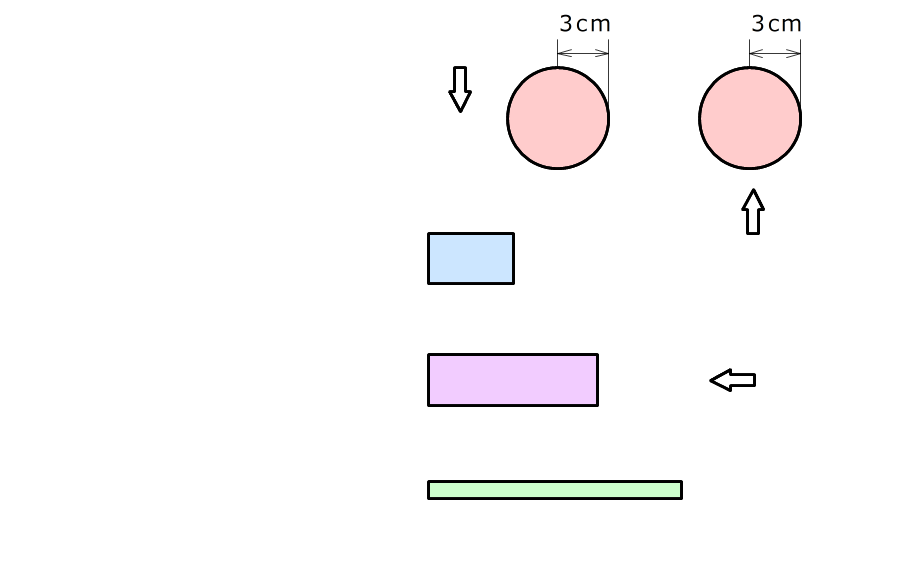
２. それぞれの図形の面積を求める
 長方形の横の長さは、底面になる円の周りの長さ
 どの面積も円周率がかかっているので、３.１４はかけずにおく

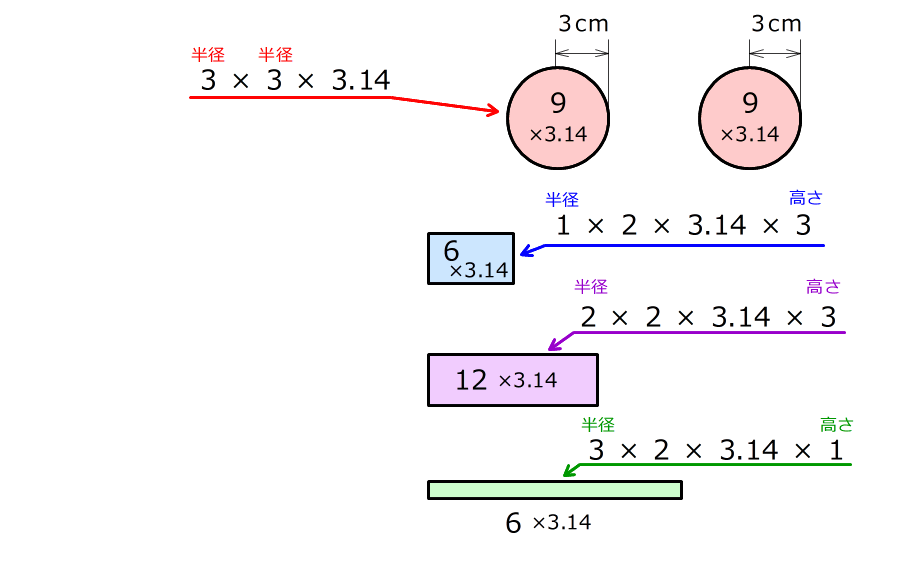
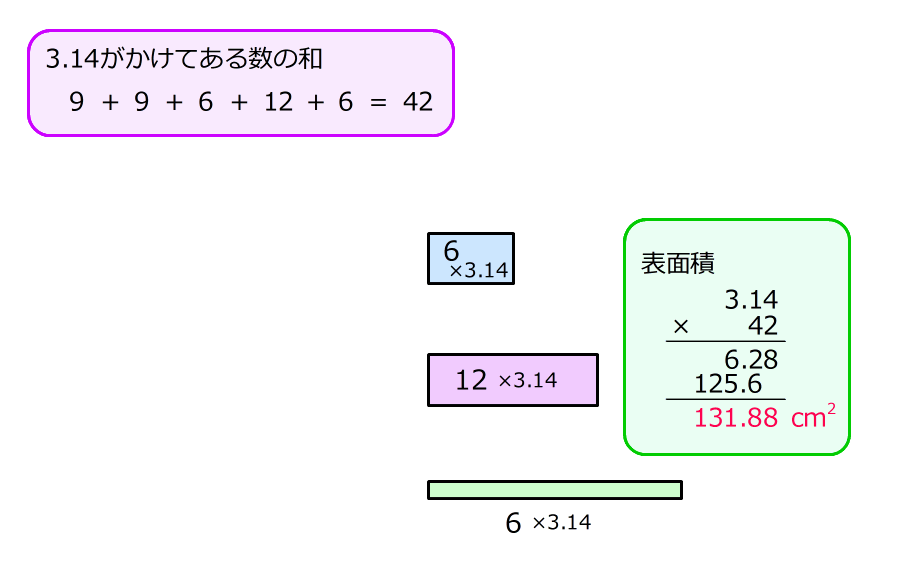
３.円周率にかかっている数を全部加えると４２
 だから、表面積は３.１４×４２で、１３１.８８㎠

（２）真ん中の円柱の水位を求める
 ４. ９０°かたむけたとき、水面が容器の上の面と下の面の真ん中を通っているので、水の量は容積の半分

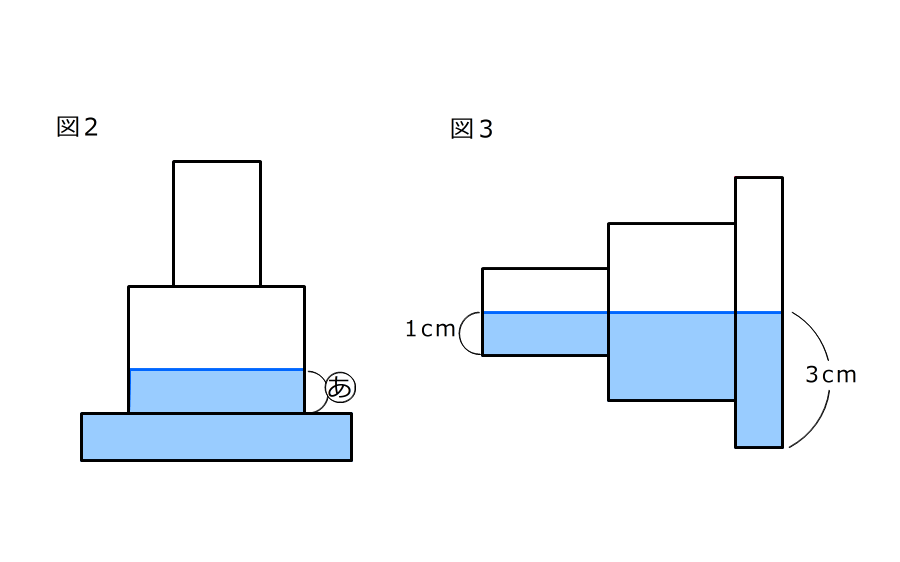
5. 容器は３つの円柱からできているのでひとつずつ容積を求めて加える
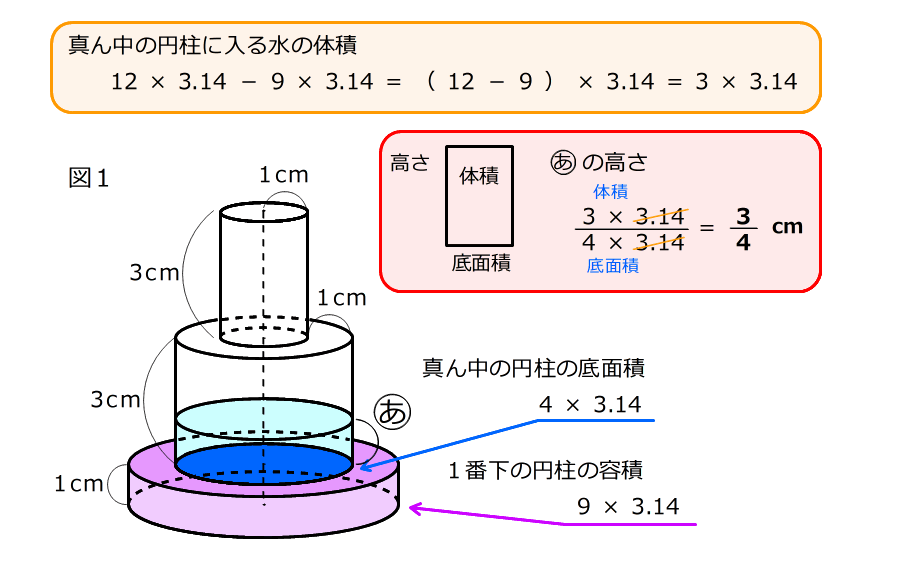
 容器の容積の半分が、水の体積

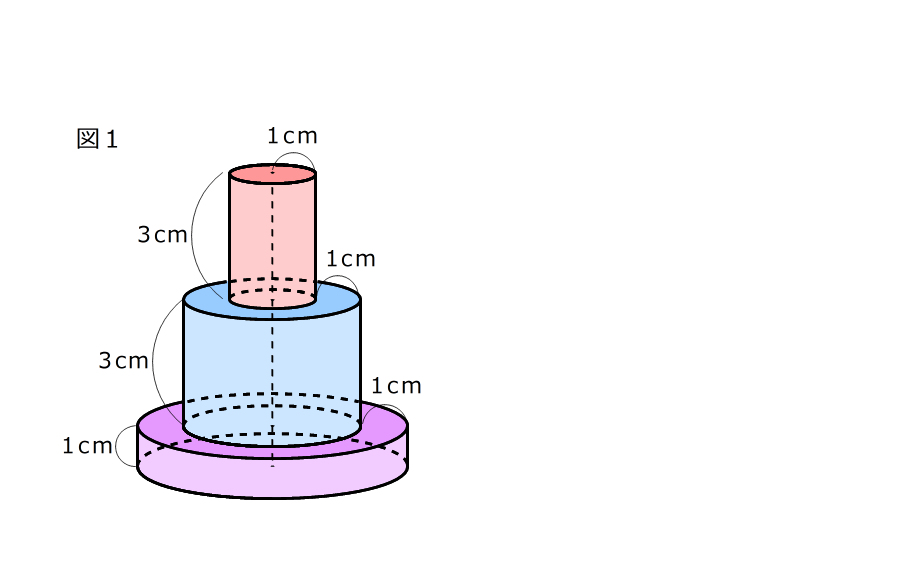
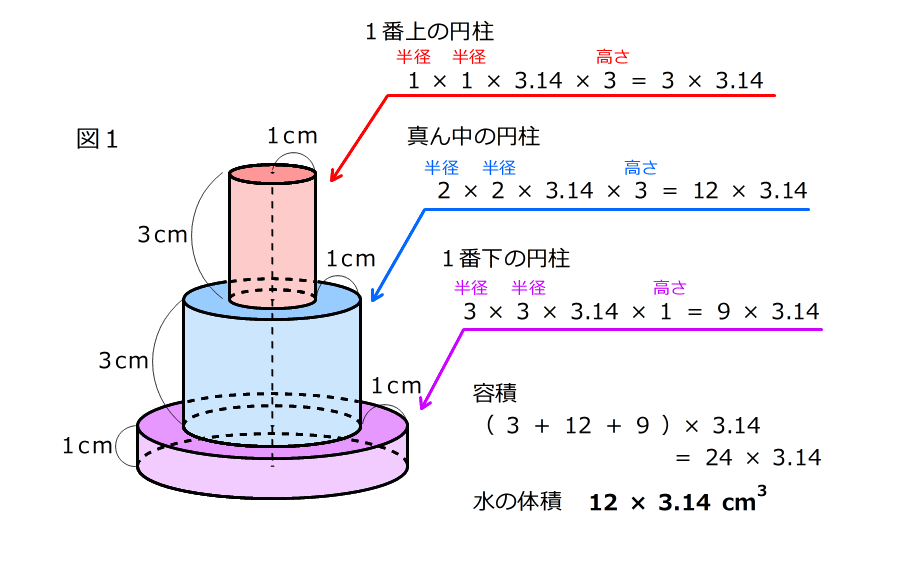
６. 真ん中の円柱に入っている水は、水全体から下の円柱の容積を除いた分
 水の体積は、底面積×高さなので、真ん中の円柱に入っている水の水位は、それを底面積で割って求める