〔9〕(18)相似図形の面積比(類題1)
(類題1)
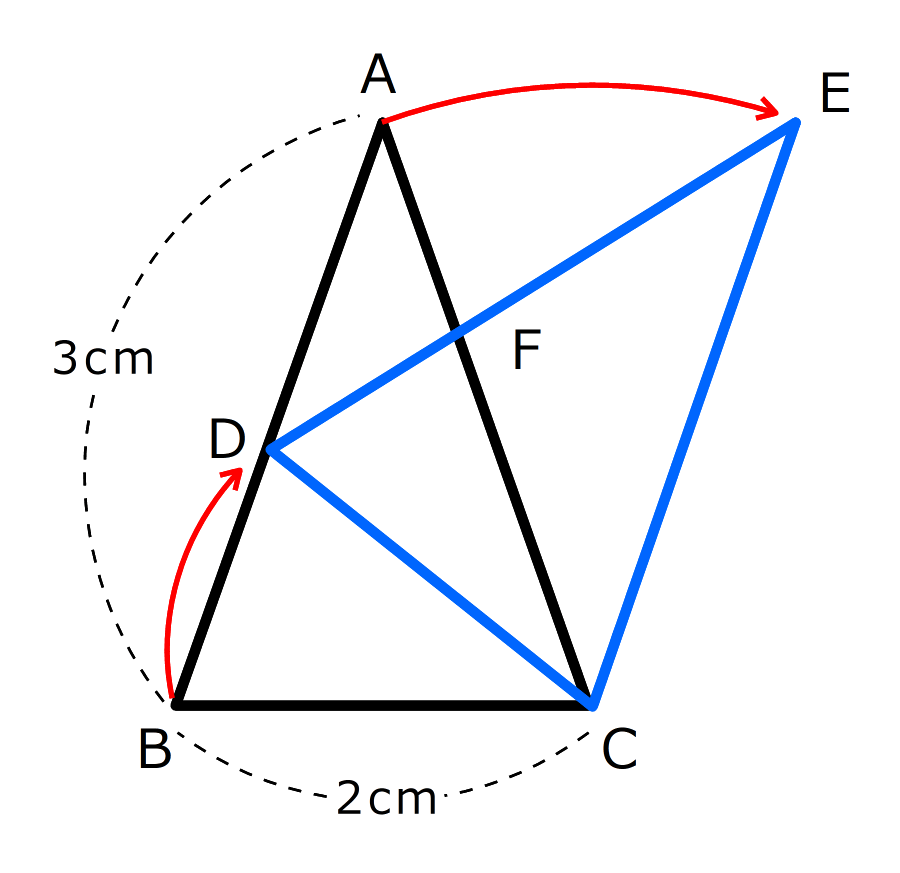
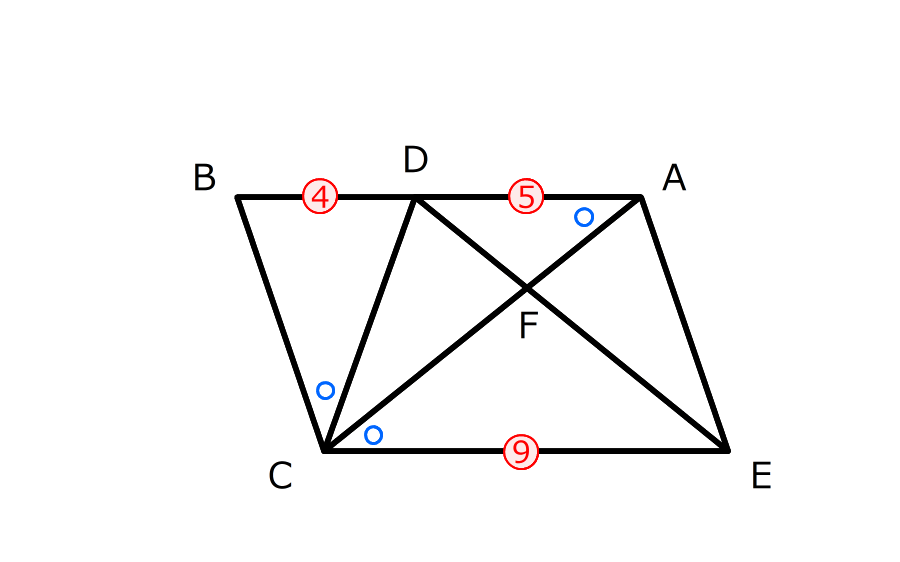
三角形ABCを、点Cを中心にして、点Bが辺AB上に来るまで回転させたところ、動く前の辺ABと、動いた後の辺AC(動いた後の点Aを点Eとしたので辺EC)が平行になりました。
三角形FDCと三角形DBCの面積の比を答えなさい。

三角形ABCを、点Cを中心にして、点Bが辺AB上に来るまで回転させたところ、動く前の辺ABと、動いた後の辺AC(動いた後の点Aを点Eとしたので辺EC)が平行になりました。
三角形FDCと三角形DBCの面積の比を答えなさい。
(クリックすると消えます)

(準備)1.相似の三角形、二等辺三角形を利用すると、辺ABと辺ECの長さが同じだと分かる


2.三角形ABCと三角形CDBが相似なので、比例式を使って、辺DBと辺ADの長さが分かる
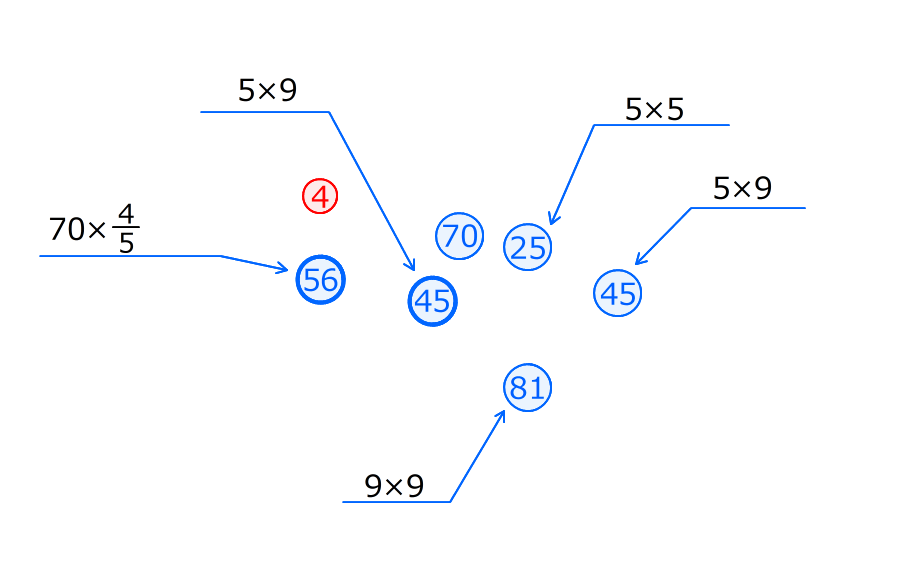
そこから、AD、DB、ECの辺の比が分かる

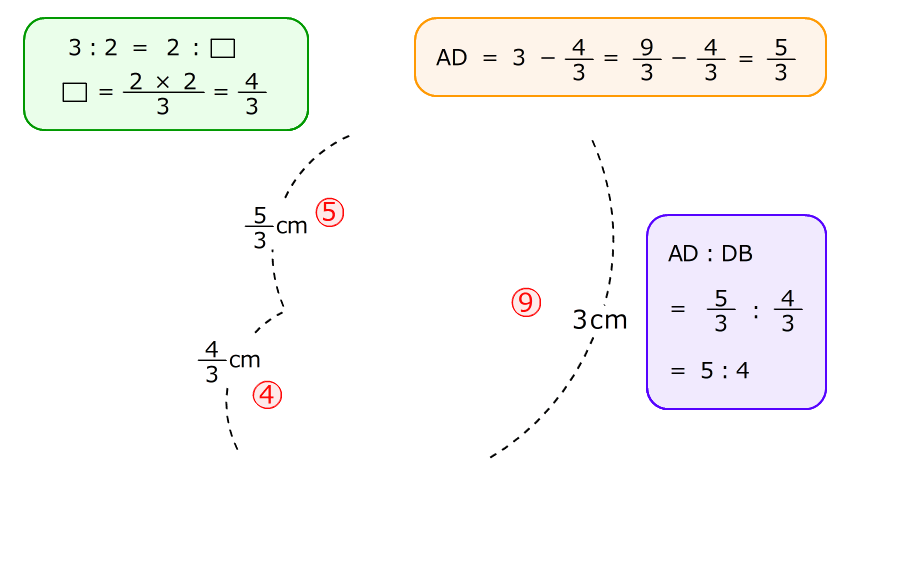

3. 上底と下底の長さの比を使って、台形の中の三角形の面積の比を求める
底辺の長さの比を使って、高さが同じ三角形の面積の比を求める