〔9〕（１8）相似図形の面積比（過去問題）
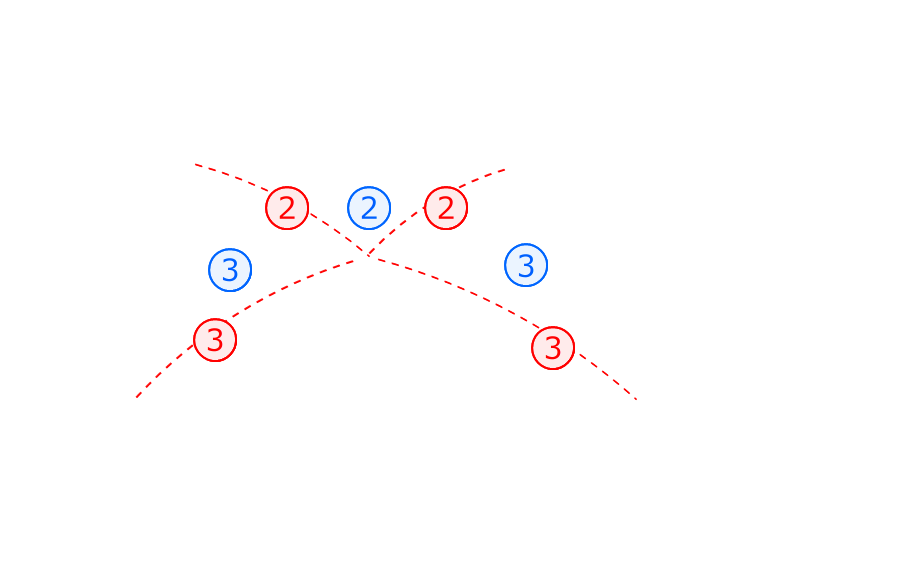
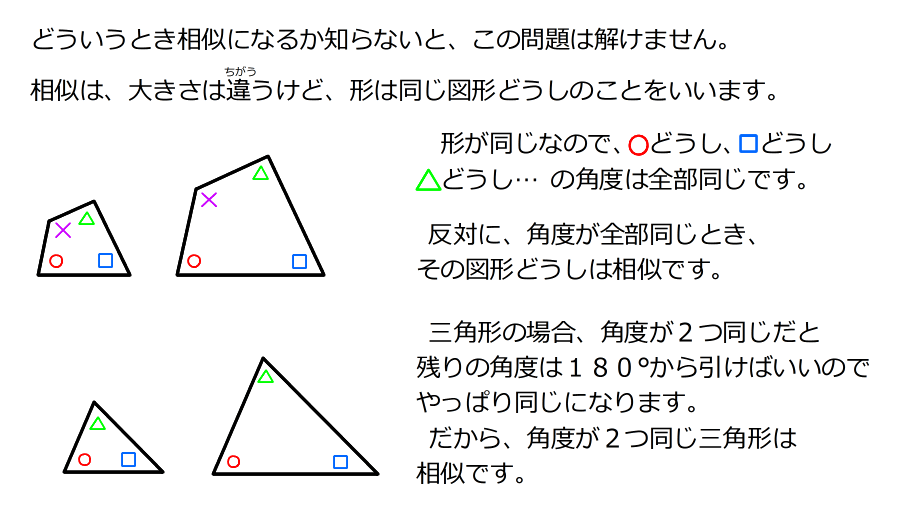
（準備１）問題の図形にかくれている相似な三角形を見つける
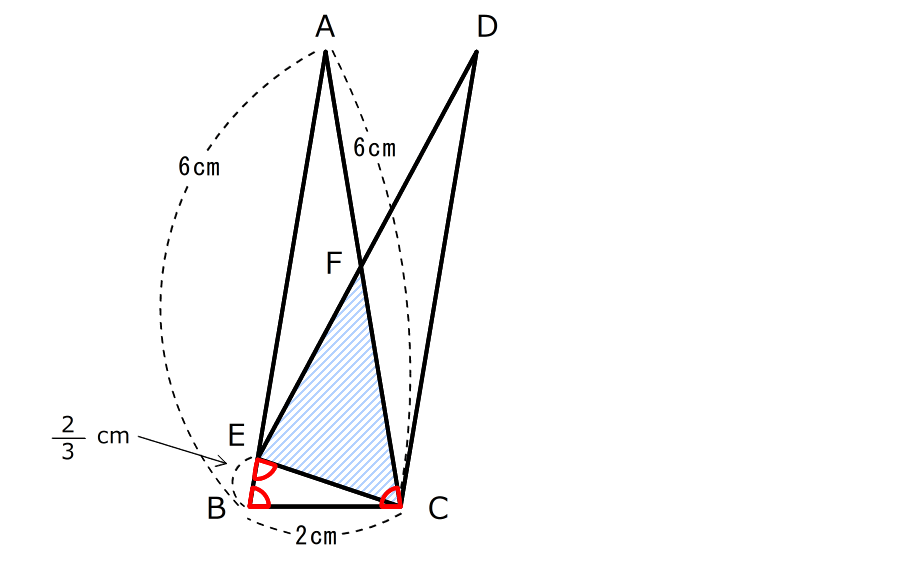
1．三角形ＡＢＣと三角形ＣＥＢが相似なことから、辺ＥＢの長さが分かる
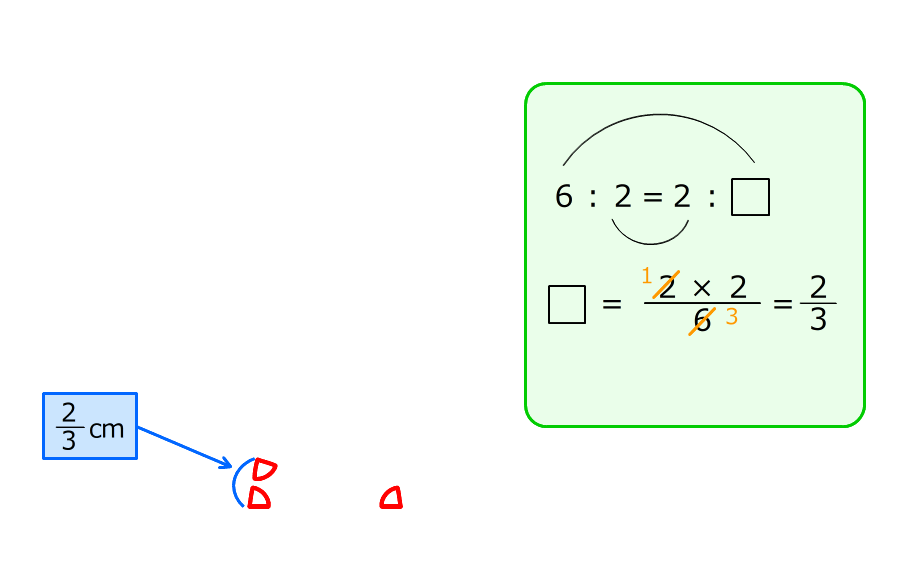
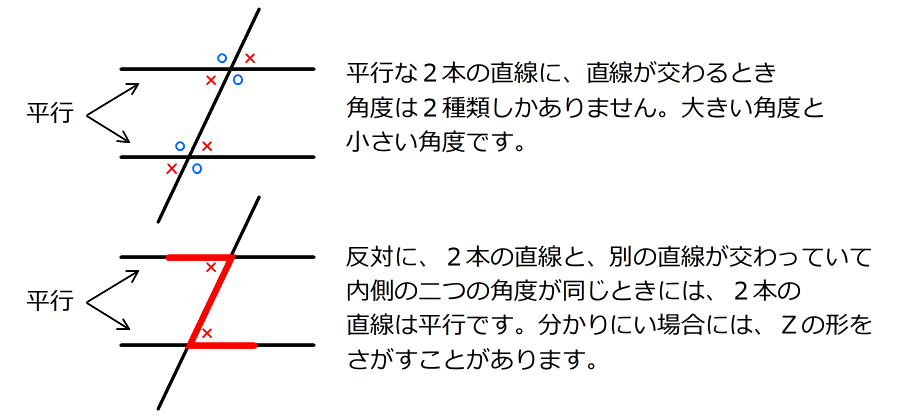
（準備２）２. 辺ＡＢと辺ＤＣが平行なので、チョウチョの形の相似な三角形がかくれている
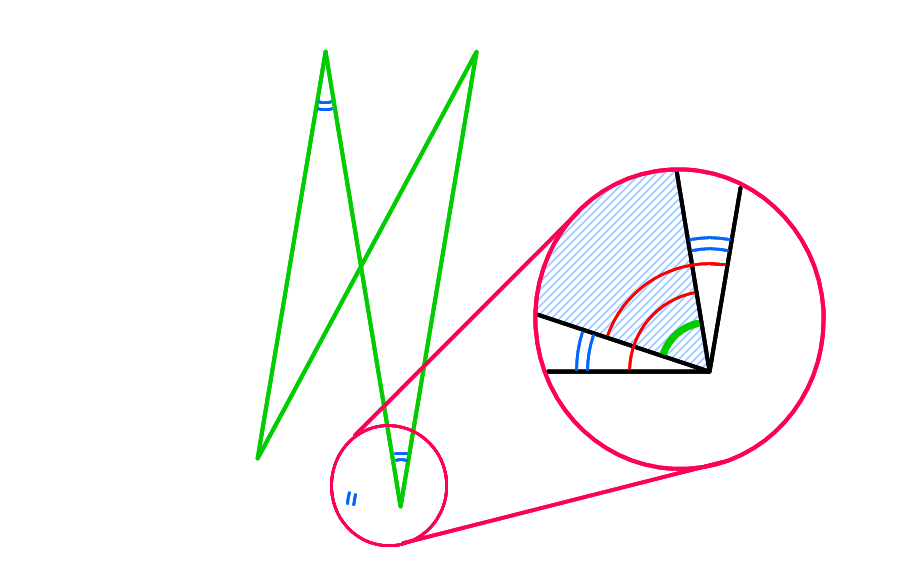
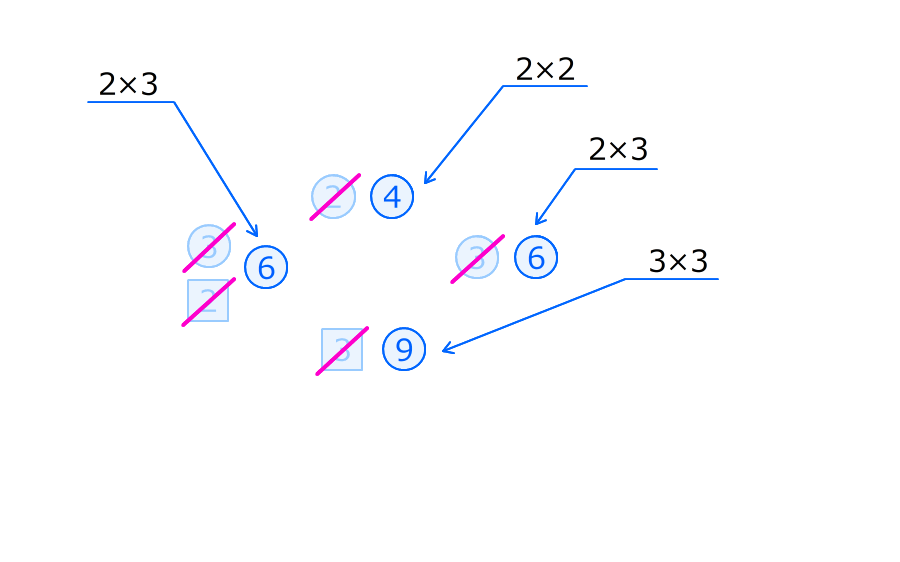
３. ＢＥ：ＡＥ＝１：８なので、台形の上底と下底の比は８：９
これを使って、台形内部の４つの三角形の面積の比を求める
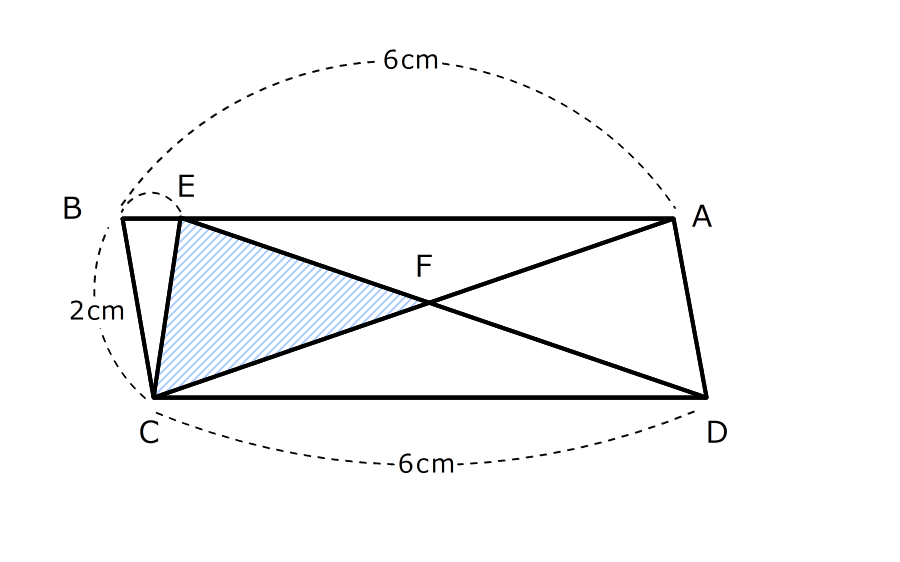
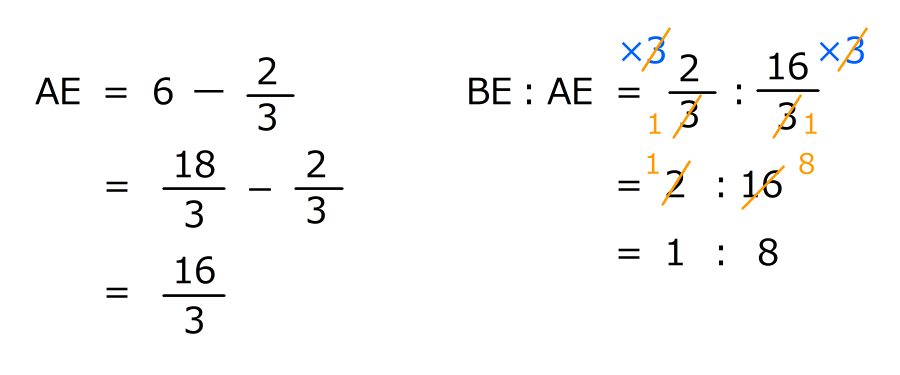
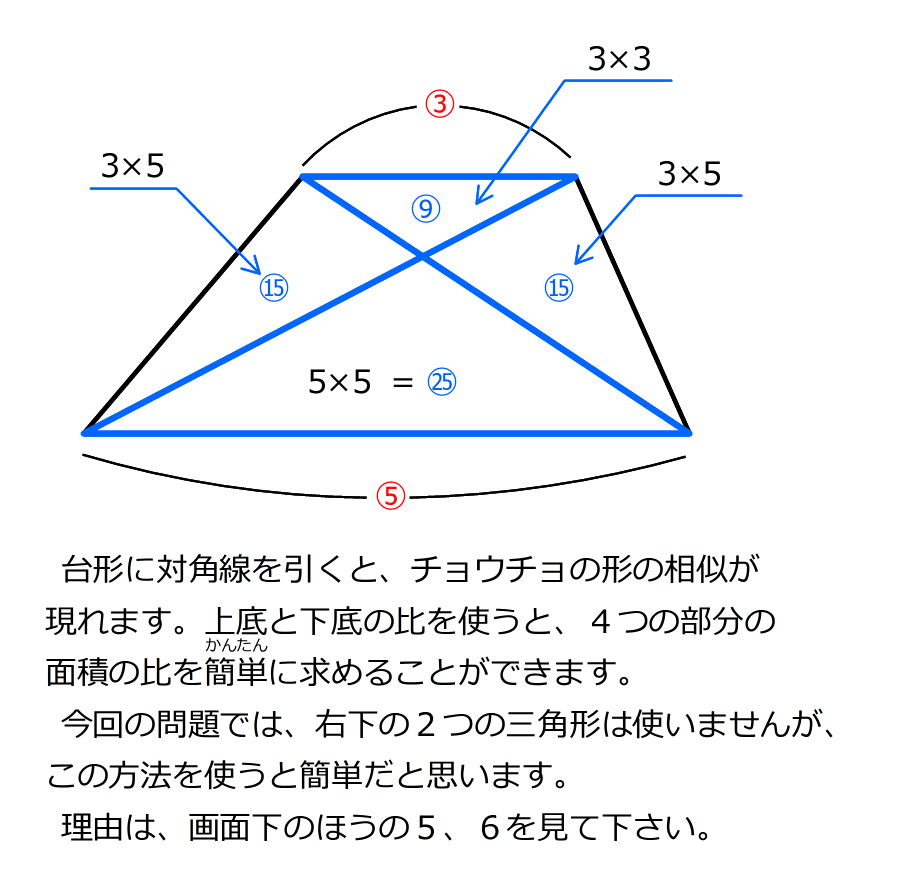
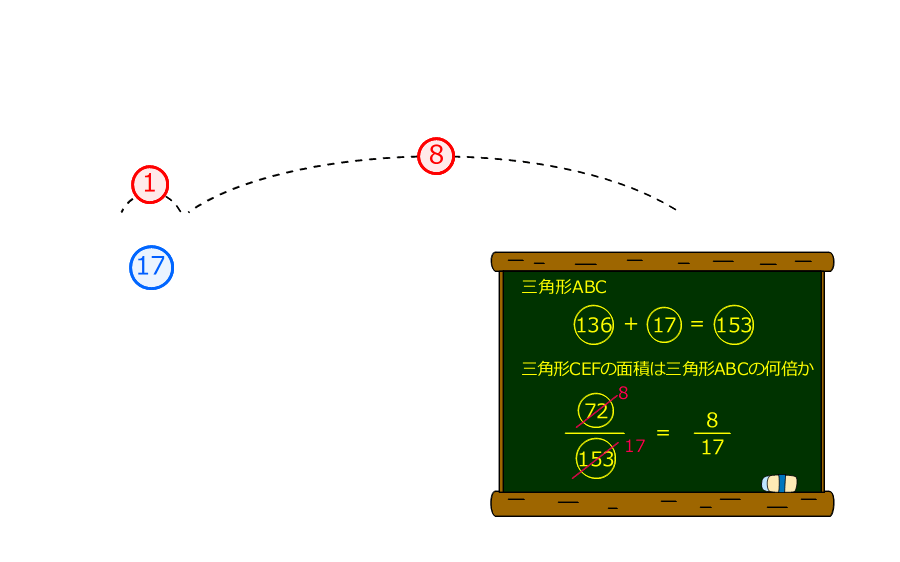
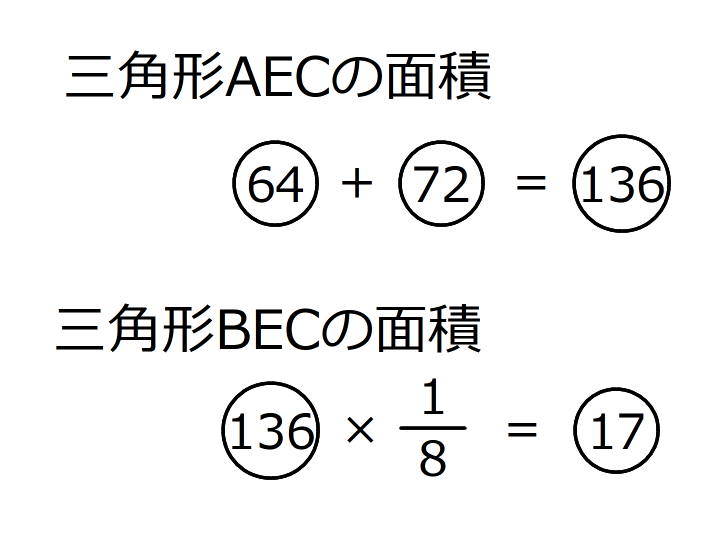
４.底辺の比を使うと、三角形ＢＥＣの面積が⑰であることが分かるので、三角形ＡＢＣの面積は
になる
三角形ＣＥＦの面積
を三角形ＡＢＣの面積で割る
（理由１）5. 高さが同じ２つの三角形の面積の比は、底辺の長さの比と同じことを使って、台形の中の上側３つの三角形の面積の比を求める
