〔3〕周期算(類題1)
(類題1)
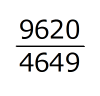 を小数で表します。
を小数で表します。
(1)小数第100位の数はいくつですか。
(2)(1)で求めた数は、小数第100位までの中に、いくつありますか。
(3)最初から数えて2020番目の2は、小数第何位の数ですか。
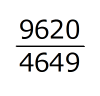 を小数で表します。
を小数で表します。(1)小数第100位の数はいくつですか。
(2)(1)で求めた数は、小数第100位までの中に、いくつありますか。
(3)最初から数えて2020番目の2は、小数第何位の数ですか。
(クリックすると消えます)

(1)小数第100位の数を求める
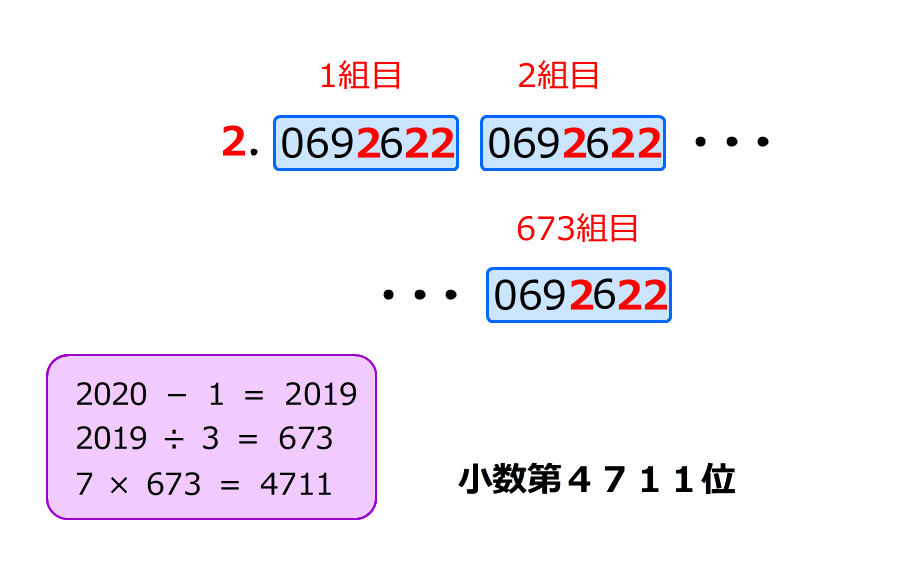
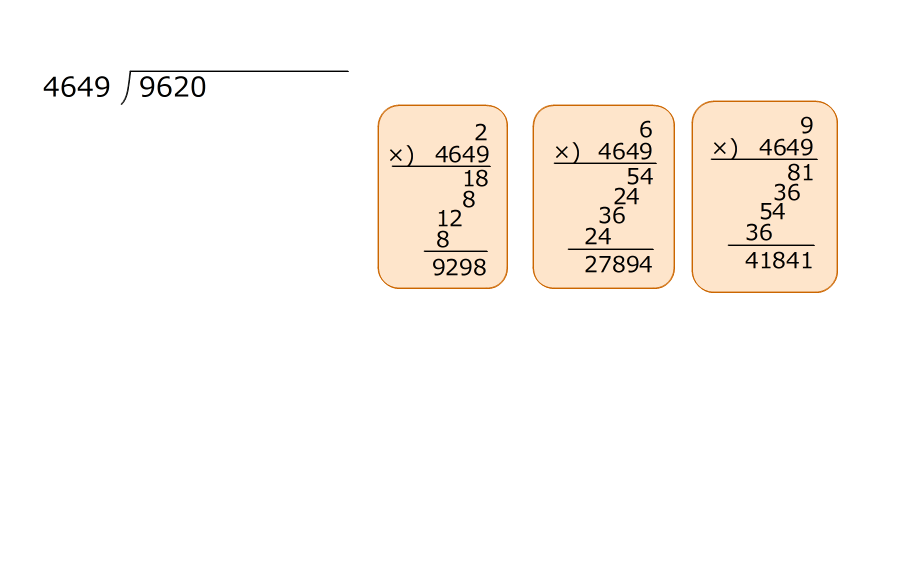
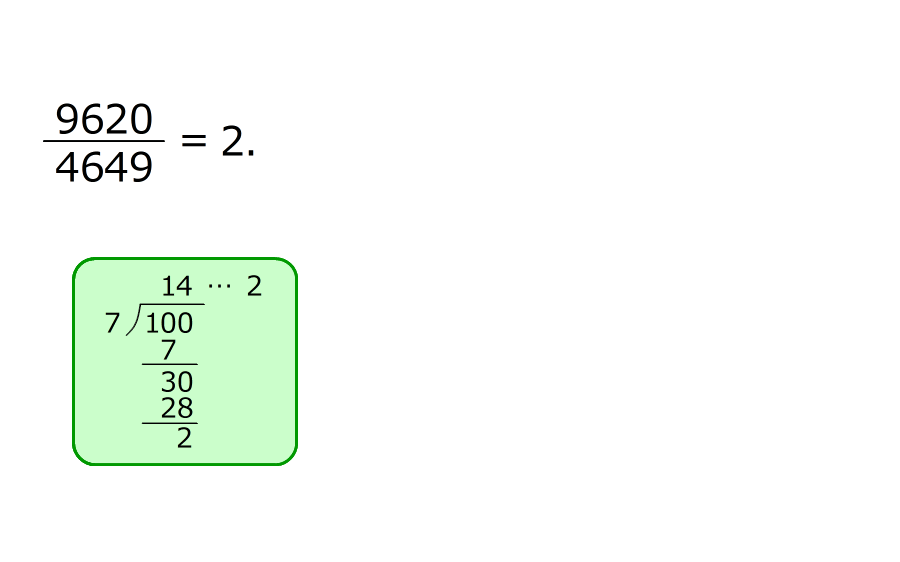
(準備)1. 割り算をすると、同じ余りが現れるので、「0692622」がくり返すことが分かる


2.100÷7=14…2なので、小数第100位までに、
「0692622」が14組あって、その後に「06」が続く
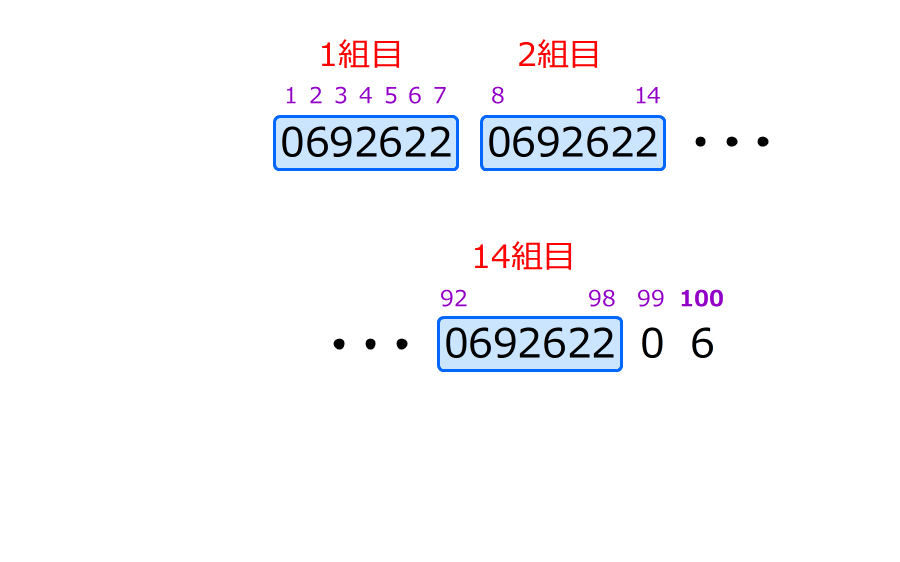

(2)小数第100位までのなかに、6がいくつあるか求める
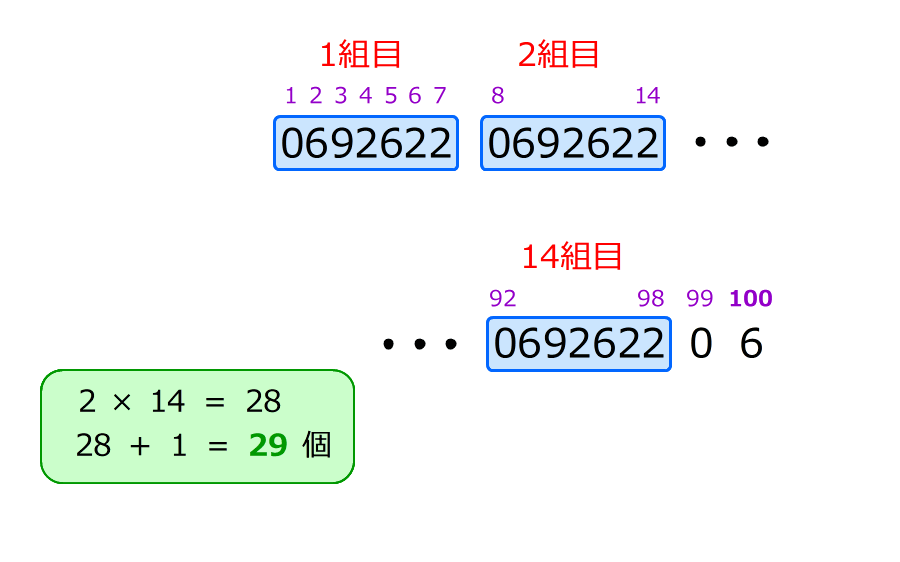
3. 14組ある「0692622」の中に「6」が2つあって、余りの中にもう1つあるので、全部で29個

(3)2020番目の2が小数第何位の数か求める
4.分数を小数に表すと1の位の数が「2」なので、2020番目の「2」は小数部分の2019番目の「2」
1組の「0692622」の中に「2」は3つある
2019÷3=673なので、2019番目の「2」は、673組の最後の数になる